1 / 14

Understanding Reflections: Lines of Symmetry and Transformations

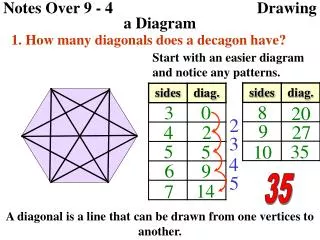
In this lesson, we explore the concept of reflections in geometry, which involves the transformation of figures over a line, known as a line of reflection. We will identify lines of symmetry in various shapes, including isosceles triangles and regular octagons. Students will practice graphing images over the y-axis and other specified lines, learning how to reflect points and figures accurately. This engaging activity encourages visual understanding of symmetry and transformations, essential for mastering geometric concepts.

harper-tyler
Télécharger la présentation

Understanding Reflections: Lines of Symmetry and Transformations

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

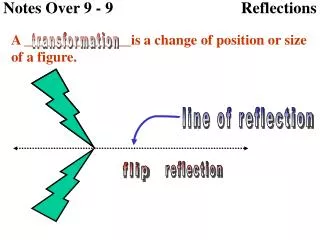
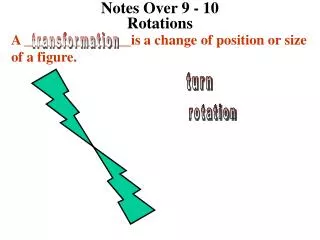
  1. Notes Over 9 - 9 Reflections A _______________is a change of position or size of a figure. transformation line of reflection reflection flip

  2. Notes Over 9 - 9 Reflections A _______________is a line that you can put inside an object to where the part of the object on one side of the line is a reflection on the other side. line of symmetry

  3. Notes Over 9 - 9 Reflections Draw all the lines of symmetry. 1. 2. isosceles triangle regular octagon 8 lines of symmetry 1 line of symmetry

  4. Notes Over 9 - 9 Reflections 3. Graph the image over the y-axis.

  5. Notes Over 9 - 9 Reflections 4. Graph the image over the line y = 2. horizontal

  6. Pg 487 9 – 9 #1 – 9, 10 – 28 Draw each figure. Draw all lines of symmetry. 1. rhombus 2. square 2 lines of symmetry 4 lines of symmetry

  7. Pg 487 9 – 9 #1 – 9, 10 – 28 Draw each figure. Draw all lines of symmetry. 3. isosceles triangle 1 line of symmetry

  8. Pg 487 9 – 9 #1 – 9, 10 – 28 Graph each point and its image over the given line. 4. R(7, 1); x-axis R R’

  9. Pg 487 9 – 9 #1 – 9, 10 – 28 Graph each point and its image over the given line. 5. S(5, - 1); y-axis S’ S

  10. Pg 487 9 – 9 #1 – 9, 10 – 28 Graph each point and its image over the given line. 6. F(- 2, 9); y = 1 • 10 • 8 • 6 • 4 • 2 • 0 • 2 • 4 • 6 • 8 • 10 F -10 -8 -6 -4 -2 0 2 4 6 8 10 F’

  11. Pg 487 9 – 9 #1 – 9, 10 – 28 Graph each point and its image over the given line. 7. N(- 4, - 6); x = 4 • 10 • 8 • 6 • 4 • 2 • 0 • 2 • 4 • 6 • 8 • 10 -6 -4 -2 0 2 4 6 8 10 12 14 N N’

  12. Pg 487 9 – 9 #1 – 9, 10 – 28 The vertices of a triangle are listed. Reflect each triangle over the given line. 8. A(0, 0), B(6, 0),C(0, - 6); y = 1 • 10 • 8 • 6 • 4 • 2 • 0 • 2 • 4 • 6 • 8 • 10 C’ A’ B’ B A -10 -8 -6 -4 -2 0 2 4 6 8 10 C

  13. Pg 487 9 – 9 #1 – 9, 10 – 28 The vertices of a triangle are listed. Reflect each triangle over the given line. 9. K(- 1, 4), L(3, 3),M(0, 2); y = 0 L K M M’ L’ K’

  14. Pg 487 9 – 9 #1 – 9, 10 – 28

More Related