1 / 25

Tree Balancing: AVL Trees

This article explores AVL trees, a self-balancing binary search tree (BST) model introduced by Russian mathematician Georgy Adelson-Velsky. We discuss the significance of keeping BSTs balanced to ensure efficient search times of O(log N). The concept of the balance factor (BF) is explained, including insertion and deletion operations that maintain balance through rotations: single (left and right) and double rotations (left-right and right-left). Examples and exercises illustrate the complexities of rebalancing AVL trees effectively.

havyn
Télécharger la présentation

Tree Balancing: AVL Trees

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Tree Balancing: AVL Trees Dr. Yingwu Zhu

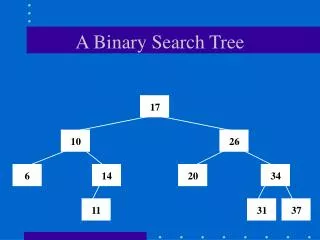
  2. Recall in BST • The insertion order of items determine the shape of BST • Balanced: search T(n)=O(logN) • Unbalanced: T(n) = O(n) • Key issue: • A need to keep a BST balanced! • Introduce AVL trees, by Russian mathematican

  3. AVL Tree Definition • First, a BST • Second, height-balance property: balance factor of each node is 0, 1, or -1 • Question: what is balance factor? BF = Height of the left subtree – height of the right subtree Height: # of levels in a subtree/tree

  4. Determine balance factor A B D C E G F H

  5. ADT: AVL Trees • Data structure to implement Balance factor Data Left Right

  6. ADT: AVL Trees • Basic operations • Constructor, search, travesal, empty • Insert: keep balanced! • Delete: keep balanced! • See P842 for class template • Similar to BST

  7. Example RI Insert “DE”, what happens? Need rebalancing? PA

  8. Basic Rebalancing Rotation • Single rotation: • Right rotation: the inserted item is on the left subtree of left child of the nearest ancestor with BF of 2 • Left rotation: the inserted item is on the right subtree of right child of the nearest ancestor with BF of -2 • Double rotation • Left-right rotation: the inserted item is on the right subtree of left child of the nearest ancestor with BF of 2 • Right-left rotation: the inserted item is on the left subtree of right child of the nearest ancestor with BF of -2

  9. How to perform rotations • Rotations are carried out by resetting links • Two steps: • Determine which rotation • Perform the rotation

  10. Right Rotation • Key: identify the nearest ancestor of inserted item with BF +2 • A: the nearest ancestor. B: left child • Step1: reset the link from parent of A to B • Step2: set the left link of A equal to the right link of B • Step3: set the right link of B to A • Examples

  11. new A B L(A) L(B) R(B) h

  12. Exercise #1 10 4 How about insert 8 20 6 9

  13. Left Rotation • Step1: reset the link from parent of A to B • Step2: set the right link of A to the left link of B • Step3: set the left link of B to A • Examples

  14. new Example A B L(A) h L(B) R(B)

  15. Exercise #2 7 18 What if insert 5 15 10 20

  16. Exercise #3 12 1 How about insert 8 16 4 10 14 2 6

  17. Basic Rebalancing Rotation • Double rotation • Left-right rotation: the inserted item is on the right subtree of left child of the nearest ancestor with BF of 2 • Right-left rotation: the inserted item is on the left subtree of right child of the nearest ancestor with BF of -2

  18. Double Rotations • Left-right rotation • Right-left rotation • How to perform? 1. Rotate child and grandchild nodes of the ancestor 2. Rotate the ancestor and its new child node

  19. Example A C What if insert B

  20. new Example A B R(A) h+1 C L(B) h+1 L(C) R(C) h

  21. Exercise #4 12 7 How about insert 8 16 4 10 14 2 6

  22. Exercise #5 4 2 6 15 What if insert 1 3 5 7 16

  23. Exercise #5 4 2 6 14 What if insert 1 3 5 15 7 16

  24. Summary on rebalancing • The key is you need to identify the nearest ancestor of inserted item • Determine the rotation by definition • Perform the rotation

More Related