A Fast Algorithm for Power Grid Design
260 likes | 400 Vues
This paper presents a fast algorithm for power grid design, focusing on optimizing wire widths and pitches while ensuring constraints for voltage drop and current density are met. By utilizing a recursive bipartitioning approach, local grids are designed efficiently, addressing practical challenges such as IR drop, electromigration, and signal integrity. The methodology allows for effective refinement of grid structures and minimizes congestion, ultimately leading to improved performance in integrated circuit designs.

A Fast Algorithm for Power Grid Design
E N D
Presentation Transcript
A Fast Algorithm for Power Grid Design Jaskirat Singh Sachin Sapatnekar Department of Electrical and Computer Engineering University of Minnesota
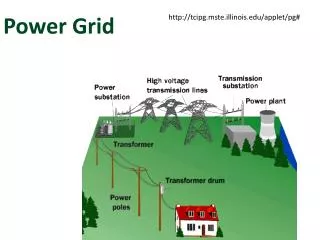
Introduction VDD • Power supply network • Provides VDD and ground to time varying current sources (logic gates) • Power grid design issues • VDD , wire width , currents • IR drop/ground bounce • Signal integrity • Gate delay • Electromigration • Mean failure time for wires GND
Introduction • Power grid design problem • Given an estimate of loading currents and power pad positions • Select a set of wire widths and pitches for the multiple-layer network so that • Wire area is efficiently utilized • Nodes (branches) satisfy voltage drop (current density) constraints • Additional objectives of congestion minimization/shielding
Non-linear optimization based method • KCL/KVL part of constraint set • Approximations needed for efficiency • May be inaccurate due to relaxations Explicit circuit simulation based method • Detect and fix method • Accurate Design • Usually slow Introduction Power grid design methods
Motivation • Notion of locality in power grid design • “Fast Flip-chip Power Grid Analysis via Locality and Grid Shell”, Eli Chiprout, ICCAD’04. • To construct local grids focus on details of local regions. Abstract far away regions of the grid.
Power Grid Abstraction Abstract away far off grid regions Fix Violations Locally • VDD pads (1V ) Locality Example • 10 X 8 Grid • Each branch 1 ohm • Loaded with 1mA • Vspec = 0.9V
High High High High High High Med Med Med Low Low Low Locally Regular/Globally Irregular • Globally regular grid • Over design of the grid • Globally irregular/locally regular grid • Efficient use of wire area • Reduced # of optimizable parameters
Divide the chip area into partitions Design local grids in the partitions Macromodeling technique by M. Zhao et al, DAC’00 Iterative refinement of grid Power Grid Design Procedure Recursive bipartitioning heuristic based on notion of locality Abstraction of grids in partitions Coarse grid representation initially Post processing step to maximize wire alignment
Vertical, horizontal partition wire Active partitions Recursive Bipartitioning Method • Divide and conquerapproach • Solve a local power grid design problem in each step k 2 2 4 1 3 3 5 K+1 2 -1
Recursive Bipartitioning Method Level-2 Partition Level-1 Partition Level-2 Partition Level-k Partition
Port Nodes First level of partitioning • Construct macromodels for the two partitions
First level of partitioning • Stamp the macromodels in the global MNA system • Solve each partition by hierarchical analysis • For violations in a partition, fix it locally • Speed up in circuit analysis step • Use very thick wires for initial partition levels • In subsequent partition levels refine the grid by reducing the wire width
Second level of partitioning • Use the power grid constructed at the first level • Rip up the grid in left partition • Add a horizontal partition wire • Leave the grid in the right partition intact, seen as an abstraction • Construct a refined grid in the top-left and bot-left partitions by the hierarchical design methodology
Second level of partitioning γ • Requirements for power grid constructed in new active partitions • IR drop and EM constraints met in the active partitions • Maintain correctness of the power grid in the right partition • Solve new global system M X=b • Compare old and new port voltages of the right partition • If Max( New_port_voltage – Old_port_voltage) > є (e.g., 1% VDD) Power grid in right partition is disturbed Add more wires in the active partitions and repeat the design procedure
Make macro Decr width by γ Make next partitions Repeat Port voltage change > є ? Recursive bipartitioning algorithm Make macro Solve by hierarchical analysis Detect violations Decr pitch by β Check neighbor port voltages Decr width by γ Make next partitions Done Post processing to align wires
γ Recursive bipartitioning algorithm Make_macromodels( ); Solve_grid( ); If(violations in one or both partitions) Decr wire pitch of violating partition; • A breakdown scenario • Min pitch violation • Grid refinement doesn’t work If (Pitch of the active partition < min_pitch) Min pitch violation; • Grids in neighboring partitions disturbed • Can’t be fixed by adding wires in active partitions • Traverse to the inactive partitions and add more wires • Adversely affects the runtime of the procedure • Empirically a rare event if γ is [ 0.65,1 ) Check_neighbor_grids( ); If(port nodes of neighbor grids perturbed) Decr wire pitch of active partition;
Post processing step • At the end of design the wires might be misaligned due to different wire pitches in adjacent partitions • Superimpose a uniform and continuous virtual grid • Pitch of the virtual grid is chosen to be the minimum pitch of all partitions • Move the real power grid wires to the nearest vacant position on the virtual grid • Perform a complete simulation by hierarchical analysis after the wire movements • Add more wires if required on the virtual grid place holders
Experimental Setup • Input • Floorplans with functional block current estimates • Power pad locations and number • Grids constructed for power delivery to 2cm X 2cm chip • Vdd=1.2V, Vspec=1.08 V • Sheet resistivity, current density, min pitch for 130nm tech • Flip-chip (FC) 400-600 power pads • Wire-bond(WB)200-300 pads located at the periphery • Initial wire width 60-100 µm, k=7 levels of partitioning • γ in (0.65,1] , β in (0.5,1], є=15mv • Output • A non-uniform power grid that meets the IR drop and EM constraints • Wire width at the end of design is 2-6 µm
Experimental Results • Power grids > 1M nodes designed in 7-12 mins for FC and 11-16 mins for WB • Wire bond designs are suboptimal due to absence of locality property
Experimental Results • Proposed method compared with a previous work K. Wang and M. M Sadowska, “On-chip Power Supply Network Optimization using Multigrid-based Technique”, DAC’04 • Multigrid method based on mapping from original space to a reduced space Multigrid Reduction Optimization engine Original mesh Reduced mesh Back mapping
% Saving in power grid wire area 7%-12% reduction in wire area over the multigrid-based method Experimental Results
High High High High High High Low Low Low Med Med Med Experimental Results • Constraints in the multigrid-based method • All rows (columns) of wires are constrained to have the same width • Wastage of wiring resources Current Densities
Experimental Results Runtime comparison of the two power grid design methods Runtime is of the same order for the two methods
Summary • A novel and efficient power grid design procedure proposed • Use notion of locality in grid design • Accuracy is maintained by using circuit analysis step in the inner loop • Circuit analysis is made efficient by the use of • Grid abstractions • Coarse initial grid models followed by successive grid refinements • Considerably fast power grid design method with efficient wire area utilization