Solids: From Bonds to Bands - Exploring Levels of Bonding and Band Formation in 1-D Solid Structures
220 likes | 239 Vues
Delve into the transition from atomic bonds to electronic bands in solids by creating minimal models for metallic or semiconducting properties. Explore the structure of 1-D chains and dimerized atoms, evolving into 3D solid systems, and study the electronic wavefunctions, eigenvalues, and effective mass within the band structure theory.

Solids: From Bonds to Bands - Exploring Levels of Bonding and Band Formation in 1-D Solid Structures
E N D
Presentation Transcript
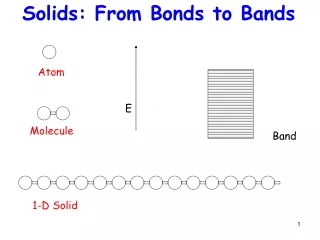
Solids: From Bonds to Bands Levels Bond Molecule Band 1-D Solid Atom E
In the spirit of ‘bottom-up’ theory, we will identify minimal models to create metallic or semiconducting bands • A simple 1-D chain of atoms with 1 electron/atom will yield a metal • A chain of dimers with 1 electron/atom will yield a semi- conductor • A real 3D solid will involve dimerization of atoms or orbitals
Recall how we went to bonds f fn-1 fn fn+1 xn-1 xn xn+1 Here ‘grid’ (or basis sets) are hydrogen 1s orbitals u1(r) and u2(r) with scalar coefficientsf1 andf2 Just as a real-space finite-diff grid gives a wave function that involves coefficients fn at diff points, this involves coefficients fn for different atomic sites f ≈ ∑ fnun(r) n
Recall how we went to bonds In this atomic basis set (rather than grid basis set), we calculate H, which becomes a matrix. The diagonal elements • = H11 = diagonal elements e -t -t e H = ∫u1(r)Hu1(r)dV, while the off- -t = ∫u1(r)Hu2(r)dV Eigenvalues e ± t (ignoring non-orthogonality) Eigenvector coefficients f1,2 = ±1/√2, ie, (u1 u2)/√2 Lower energy state occupied by electrons ± in this atomic basis set
-t e e -t e -t -t e -t H = -t e -t 1-D Solid Extend now to infinite chain e: Onsite energy (2t+U) -t: Coupling (off-diag. comp. of kinetic energy) Note how this looks like the Finite-element H !
-t e e -t e -t -t e -t H = -t e -t 1-D Solid Extend now to infinite chain Let’s now find the eigenvalues of H for different matrix sizes N This is because our basis sets are localized on atoms and look like grid points
N=2 4 6 8 10 20 50 500 Eigenspectra If we simply find eigenvalues of each NxN [H] and plot them in a sorted fashion, a band emerges! Note that it extends over a band-width of 4t (here t=1). The number of eigenvalues equals the size of [H] Note also that the energies bunch up near the edges, creating large DOS there
Eigenspectra If we simply list the sorted eigenvalues vs their index, we get the plot below. Can we understand this analytically ?
Simplify algebra E k k The results are not sensitive to boundary conditions, as seen above But periodic bcs make the algebra simple. Let’s now look at the equation for the nth row. -t(fn+1 + fn-1 -2fn) = Efn Periodicity allows us to try a solution fn = f0eikna, substituting which gives us E = 2t[1-coska]
2p/a f(x) f1 f3 f2 f4 x2 x3 x4 x1 Band properties E = 2t[1-coska] gives us a band of states. (a) Need to go only upto ka = p (Brillouin Zone) (b) Band bottom at k=0 (value 0) and top at ka=p (value 4t) (c) Bandwidth = 4t depends on overlap between atoms Equiv states as far as coeffs go
Band properties + + + + Periodic nuclear potential
Band properties Electronic wavefunctions overlap and their energies form bands
Band properties Shallower potentials give bigger overlaps. Greater overlap creates greater bonding-antibonding splitting of each multiply degenerate level, creating wider bandwidths Since shallower potentials allow electrons to escape easier, they correspond to smaller effective mass Thus, effective mass ~ 1/bandwidth ~ 1/t (t: overlap)
Effective Mass Near bottom of band, can fit a parabola • So Effective Mass m* = ħ2/(∂2E/∂k2) ~ 1/curvature of E-k • In case of our 1-D band E=2t(1-coska), m* = ħ2/2ta2 (~ 1/t, as argued earlier) • Electronic properties at low bias depend on these effective masses • Eg. GaAs m* = 0.067 me, Si ml*=0.91me, mt* = 0.19 me But instead of using a free electron mass to calculate t (chapter 2), we are using a differently computed t (overlap of basis sets un) to extract m*. This does not need to match the free electron mass!! In fact it incorporates nuclear attraction terms effectively.
Effective Mass Effective Mass m* = ħ2/(∂2E/∂k2) Larger E-k curvature means smaller m* (Steeper bowl in k-space gives mobile electrons) Is that sensible? Recall that x and k are Fourier transforms This means that a steeper parabola in k-space actually corresponds to a shallower bowl-shaped potential in real space, which an electron can easily get out of. This corresponds to a more mobile electron with a smaller m* and a larger band-width t.
Approximations to bandstructure Properties important near band tops/bottoms
Filling these band states Periodic bcs mean exp(ikL) = exp(ikNa) = 1 kL = 2pn (n=0,1,2,…,N-1) N sites give N states, and N electrons
Filling these band states But each state can accommodate two electrons (up and down spins) So only half the states are filled EF near band middle where lot of states exist METAL N sites give N states, and N electrons
≈ ∑ fnun(r) with fn = f0eikna Coeffs for a particular eigenstate with a Specific k f1 f3 f2 f4 x2 x3 x4 x1 u1 u2 un-1 un What do the wavefunctions look like? u(x) f2 f4 x2 x3 x4 x1
≈ ∑ fnun(r) with fn = f0eikna What do the wavefunctions look like? f(x) x2 x3 x4 x1 Bloch solutions (part ‘atomic’ through u’s and part plane wave through fns)
+ + + + + + + + + E E + + + + - - - - k k Conduction Band Valence Band This flips the sign of t To get both bands, need two diff basis sets (e.g. s and px), or equivalently, two different types of atoms