1 / 9

Understanding Special Right Triangles: 45°-45°-90° and 30°-60°-90° Properties

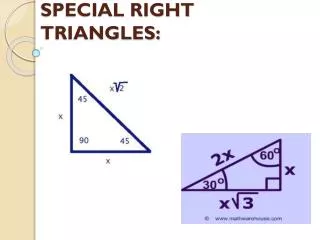
This guide explores the properties and relationships of special right triangles, specifically the 45°-45°-90° and 30°-60°-90° triangles. It discusses how the legs of the 45° triangle are congruent, with the hypotenuse being the leg length multiplied by √2. For the 30°-60°-90° triangle, it describes how the hypotenuse is twice the shorter leg, and the longer leg is the shorter leg multiplied by √3. Key example calculations are provided to demonstrate these concepts using specific leg measurements.

jamal
Télécharger la présentation

Understanding Special Right Triangles: 45°-45°-90° and 30°-60°-90° Properties

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Special Right Triangles 45° 45° 90° and 30° 60° 90°

  2. 45° Y X 45° X Z The legs are congruent because sides opposite congruent angles are congruent

  3. Legs are congruent Hypotenuse = leg times the √2 hypotenuse leg leg

  4. Y 12ft 8in X 45° 45° X Y X= 6√2 ft X= 8in Y= 6√2 ft Y= 8√2 in

  5. 2X 2X Y X 2X The two right triangles are congruent so Z=2X 60° Z Z 60° 60° Z

  6. Hypotenuse = 2 short legs Long leg = short leg • 3 Hypotenuse Long Leg 60° Short Leg

  7. Y 16 X Y 60° 60° 7 X 16=2X X = 7√3 Y = 14 X = 8 Y = 8√3

  8. Y Y 5√3 9 60° 60° X X 5√3=X√3 X = 3√3 Y = 6√3 X = 5 Y = 10

More Related