1 / 31

Binary Search

Binary Search.

jglick
Télécharger la présentation

Binary Search

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

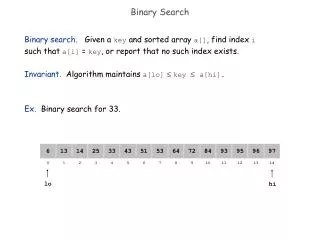
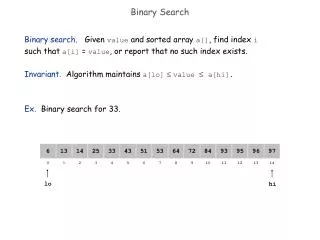
  1. Binary Search A binary search algorithm finds the position of a specified value within a sorted array. Binary search is a technique for searching an ordered list in which middle item is checked first and - based on that comparison – half of the data is discarded. The same procedure is then applied to the remaining half until a match is found or there are no more items left. • Course Name: Design and Analysis of Algorithms Level(UG/PG): UG • Author : Phani Swathi Chitta • Mentor : Aruna Adil *The contents in this ppt are licensed under Creative Commons Attribution-NonCommercial-ShareAlike 2.5 India license

  2. Learning Objectives After interacting with this Learning Object, the learner will be able to: • Explain how to find an element in an array using “Binary Search”

  3. Definitions of the components/Keywords: 1 • Binary Search is also calledhalf-interval search algorithm. • The binary search is best suitable search algorithm for searching a particular value in sorted arrays. • Every iteration eliminates half of the remaining possibilities because the array is sorted. This makes binary searches very efficient - even for large arrays. • Desired element / Item / Search value: An element that is being searched for in the array. 2 3 4 5

  4. Definitions of the components/Keywords: 1 • Process to find the desired element using Binary search: • Length of the array is defined. • Get the middle element -----> floor[(start + end)/2] • start: Index of the first element • end: Index of the last element • If the middle element equals to the searched value, the algorithm stops; • otherwise, two cases are possible: • If searched value is less than the middle element, restrict the search to the first half (start to mid -1) of the list • If searched value is greater than the middle element, restrict the search to the second half (mid + 1 to end) of the list • Repeat steps 2 and 3 until • searched element is found or • sub array has no elements. This implies element is not found in the array 2 3 4 5

  5. Definitions of the components/Keywords: • Algorithm to implement binary search: • int binarySearch(int arr[ ], int value, int start, int end) • { •       while (start <= end) • { •             int middle = floor(start + end) / 2; •             if (arr[middle] == value) •                   return middle; •             else if (arr[middle] > value) •                   end = middle - 1; •             else •                   start = middle + 1; •       } •       return key_not_found; • } 1 2 3 4 5

  6. Definitions of the components/Keywords: 1 • The advantage of binary search is its speed of finding the desired element in large arrays when compared to sequential search. • The main limitation of binary search is that it can be done only on sorted arrays. • The complexity of any searching method is determined from the number of comparisons performed among the elements of the list in order to find the element. • The time required for a search operation depends on the complexity of the searching algorithm. • The complexity of the binary search algorithm is O(log n). 2 3 4 5

  7. Master Layout 1 • Give START, PAUSE and STOP buttons • Give 2 radio buttons • Element found • Element not found • Give a STEPPER button that allows the user to follow the simulation procedure step by step. After every step the simulation pauses until the STEPPER button is pressed • Give a text area to display the status of the simulation • Give a slider bar to control the speed of animation Simulation Area 0 Index 2 0 1 2 3 4 5 6 7 3 Array or list Fig. A 4 Current Indices: Give the value of the Indices i, j and mid at that particular time Legend: Array Desired element Desired element Match Current Index 5 ** For animator: All digits written in white in the array are “elements” or “values at index n “(n refers to index number ex. value at index 4 = 14).

  8. Step 1: Case – 1 (Element Found) 1 j=7 i=0 0 1 2 3 4 5 6 7 start end 2 start: i=0 end: j=7 mid: FLOOR ([0+7]/2) = 3 3 Legend: Array Desired element Desired element Match Current Index Search Value: 4 5

  9. Step 2: 1 i=0 mid=3 j=7 0 1 2 3 4 5 6 7 start end 2 Comparing 21 and 25 start: i=0 end: j=7 mid: 3 3 Legend: Array Desired element Desired element Match Current Index Search Value: 4 5

  10. Step 3: 1 0 1 2 3 4 5 6 7 i=0 j=2 2 0 1 2 start: i=0 end: j= mid -1 = 3-1= 2 mid: FLOOR ([0+2]/2) = 1 start end 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  11. Step 4: 1 0 1 2 3 4 5 6 7 i=0 mid=1 j=2 start: i=0 end: j=2 mid: 1 0 1 2 2 start end Search Value: 3 Legend: Array Desired element Desired element Match Current Index Comparing 21 and 14 4 5

  12. Step 5: 1 0 1 2 3 4 5 6 7 0 1 2 start: i=mid +1 = 1+1 = 2 end: j=2 mid: FLOOR ([2+2]/2) = 2 2 i=2 j=2 2 start end 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  13. Step 6: 1 0 1 2 3 4 5 6 7 0 1 2 start: i=2 end: j=2 mid: 2 2 mid=2 i=2 j=2 2 Search Value: 3 start end Legend: Array Desired element Desired element Match Current Index Comparing 21 and 21 Element found at location 2 4 5

  14. Step 7: Case – 2 (Element not found) 1 j=7 i=0 0 1 2 3 4 5 6 7 start end 2 start: i=0 end: j=7 mid: FLOOR ([0+7]/2) = 3 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  15. Step 8: 1 i=0 mid=3 j=7 0 1 2 3 4 5 6 7 start end 2 start: i=0 end: j=7 mid: 3 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  16. Step 9: 10: i=0 mid=3 j=7 1 0 1 2 3 4 5 6 7 start end 2 start: i=0 end: j=7 mid: 3 Comparing 65 and 25 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  17. Step 10: 1 0 1 2 3 4 5 6 7 i=4 j=7 4 5 6 7 2 start end start: i=mid +1 = 3+1 = 4 end: j= 7 mid: FLOOR ([4+7]/2) = 5 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  18. Step 11: 1 0 1 2 3 4 5 6 7 i=4 j=7 mid=5 4 5 6 7 2 start end start: i=4 end: j= 7 mid: 5 3 Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  19. Step 12: 1 0 1 2 3 4 5 6 7 i=4 j=7 mid=5 4 5 6 7 2 start: i=4 end: j= 7 mid: 5 start end 3 Search Value: Comparing 65 and 52 Legend: Array Desired element Desired element Match Current Index 4 5

  20. Step 13: 1 0 1 2 3 4 5 6 7 4 5 6 7 start: i=mid+1 = 5+1 = 6 end: j= 7 mid: FLOOR ([6+7]/2) = 6 2 i=6 j=7 6 7 end 3 start Search Value: Legend: Array Desired element Desired element Match Current Index 4 5

  21. Step 14: 1 0 1 2 3 4 5 6 7 4 5 6 7 start: i=6 end: j= 7 mid: 6 2 mid=6 j=7 i=6 6 7 3 Search Value: end start Legend: Array Desired element Desired element Match Current Index 4 5

  22. Step 15: 1 0 1 2 3 4 5 6 7 4 5 6 7 2 start: i=6 end: j= 7 mid: 6 mid=6 j=7 i=6 6 7 3 end start Search Value: Legend: Array Desired element Desired element Match Current Index Comparing 65 and 60 4 5

  23. Step 16: 1 0 1 2 3 4 5 6 7 4 5 6 7 2 start: i=mid+1 = 6+1 = 7 end: j= 7 mid: FLOOR ([7+7]/2) = 7 6 7 i=7 j=7 3 Search Value: 7 start end Legend: Array Desired element Desired element Match Current Index 4 5

  24. Step 17: 1 0 1 2 3 4 5 6 7 4 5 6 7 2 6 7 start: i=7 end: j= 7 mid: 7 3 mid=7 i=7 j=7 7 Search Value: start end Legend: Array Desired element Desired element Match Current Index 4 5

  25. Step 18: 0 1 2 3 4 5 6 7 1 4 5 6 7 start: i=0 end: j= 7 mid: 7 2 6 7 mid=7 Search Value: i=7 j=7 3 Legend: Array Desired element Desired element Match Current Index 7 start end Comparing 65 and 76 4 5

  26. Electrical Engineering Slide 1 Slide 3 Slide 27-30 Slide 31 Introduction Definitions Analogy Test your understanding (questionnaire)‏ Lets Sum up (summary)‏ Want to know more… (Further Reading)‏ Interactivity: Try it yourself Array Size : Values in the array: : • Give a dropdown to select the array size from 2- 8 . • Place an input box and an ENTER button to enter the values in the array. • After ENTER is pressed, show the array with indices on the top in the simulation area. • Give another input box to enter the desired element value • After the desired element value is entered, show the value in the simulation area. • After desired element value is shown, enable START button. • Once the animation is started, then enable PAUSE and RESET buttons. Desired element Value : In the input box the user will input all the numerical values that he/she wants to be in the array. 26 Credits

  27. Questionnaire 1 • Which of the following are TRUE about Binary search? • It is a sequential search • Its complexity is O(log n) • It is also called half- interval search Answers: a) I and II b) Only II c) II and III d) I, II and III 2 3 4 5

  28. Questionnaire 1 2. For a searching operation to be done using binary search, the array must be Answers: a) Sorted b) Unsorted c) either sorted or unsorted 2 3 4 5

  29. Questionnaire 1 • 3. The following statement is TRUE/ FALSE • Binary search is very efficient for large arrays. Answers: a) TRUE b) FALSE 2 3 4 5

  30. Questionnaire 1 4. Binary search takes more comparisons than linear search to find an element Time taken to find an element is more and is the main disadvantage in binary search which of the above are TRUE? Answers: a) I and II b) Only I c) Only II d)None 2 3 4 5

  31. Links for further reading Reference websites: http://en.wikipedia.org/wiki/Binary_search http://video.franklin.edu/Franklin/Math/170/common/mod01/binarySearchAlg.html Books: “Introduction to Algorithm” Thomas H. Coremen

More Related