1 / 40

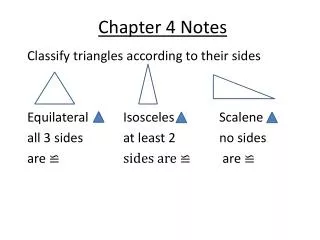
Chapter 4 Notes

Chapter 4 Notes. Graphing Linear Equations and Functions. 4.1 Coordinates and Scatter Plots. Objectives: -Plot points in a coordinate plane -Draw scatter plots and make predictions about the data. Terms. Coordinate Plane Ordered pair X-coordinate Y-coordinate.

karolynr
Télécharger la présentation

Chapter 4 Notes

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Chapter 4 Notes Graphing Linear Equations and Functions

  2. 4.1 Coordinates and Scatter Plots Objectives: -Plot points in a coordinate plane -Draw scatter plots and make predictions about the data

  3. Terms • Coordinate Plane • Ordered pair • X-coordinate • Y-coordinate

  4. Labeling the Coordinate plane

  5. Plotting Points • Plot the following points • (0,3) • (-2, -1) • (2,0) • (4,5)

  6. Locating Quadrants Find the quadrant of the following points • (0,3) • (-2, -1) • (2,0) • (4,5)

  7. Making a Scatter Plot

  8. 4.2 Graphing Linear Equations Part1 Objectives: -Make a list of values for a given equation

  9. Terms • Solution of an Equation • Function Form

  10. Function Form • Rewrite the equations in function form (y=mx+b) • -3x + y = 12 • 2x + 3y = 6

  11. Function Form • Rewrite the equations in function form (y=mx+b) • -x – y = 5 • 5x + 5y = 20

  12. T-Charts • Rules for t-Charts • Equations must be in function form • Choose numbers for x • Substitute them in for x • Solve for y • Repeat to get a total of 3 values for your function

  13. T-Charts • Make a table of values(T-Chart) for each function • Y = -2x – 6 y = 3(6x – 1) X Y X Y

  14. T-Charts • Make a table of values(T-Chart) for each function • Y = 3x - 5 y = 7 – 4x X Y X Y

  15. When the equation has an X but no Y Ex: x = 5 When the equation has a y but no x Ex: y = 8 Special Cases

  16. 4.2 Graphing Linear Equations Part2 Objectives: -Graph linear equations and make t- charts

  17. T-Charts • Rules for t-Charts • Equations must be in function form • Choose numbers for x • Substitute them in for x • Solve for y • Graph the values

  18. Graphing • Y = 4x – 2 y = 2(x – 1) X Y X Y

  19. Graphing • 2x + 2y = 10 5x – 7 = 5y X Y X Y

  20. 4.3 Quick Graphs Using Intercepts Objectives: -Find the x and y intercepts -graph a linear equation using the x and y intercepts

  21. Terms • X- intercept • Y- intercept

  22. Finding the x-intercept • X-intercepts always have ordered pairs in the form (#,0) • To find the x-intercept you plug 0 in for y and solve for x.

  23. Finding the y-intercept • y-intercepts always have ordered pairs in the form (0,#) • To find the y-intercept you plug 0 in for x and solve for y.

  24. Practice • Given the x and y intercepts graph the equation • x-intercept = 2; x-intercept = -4; y-intercepts = -3 y-intercepts = 5

  25. 5x + 4y = -20 6x – y = 6 Finding x and y -intercept

  26. -3x + y = -6 3x – y = -2 Finding x and y -intercept

  27. 4.4 Slope Objectives: -Find the slope of a line given 2 pts

  28. Terms • Slope • Rate of change

  29. Finding Slope form a Graph A B

  30. Finding Slope with a Formula Slope = change in y change in x

  31. Special cases • #/0 means slope = undefined (U) • 0/# means slope = 0

  32. (2,3)(4,-5) (1,-5)(-5,2) (3,6)(3,0) (0,5)(7,5) Practice

  33. (4,1)(6,-3) (2,2)(-3,5) (-6,-1)(-6,-4) (0,-10)(-4,0) Practice

  34. White Board Practice • One person from each row get white boards and accessories

  35. 4.6 Quick Graphs Using Slope Intercept Objectives: -Graph a linear equation in slope intercept form

  36. Terms • Slope-intercept form • Parallel lines • Perpendicular Lines

  37. Locating slope and intercept • Given an equation in y=mx+b form • m=slope (pattern) b= y-intercept (start pt.) • Slope must be a fraction !!!

  38. How it works • 1st you start on the y axis at the b value • 2nd you use your slope to rise and run from the b value

  39. Graph each of the following and tell the slope and intercept Y = 2x – 3 Y= -3x – 2 Y= ½ x + 5 Practice

  40. Graph each of the following and tell the slope and intercept Y= 2/3x – 1 Y= 2x 2y + 3x = 6 Practice

More Related