1 / 10

Understanding Proportions and Cross Products in Ratios

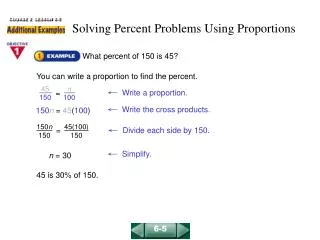
In this lesson, we will learn how to solve proportions using the cross product method. The cross product is obtained by multiplying the numbers diagonally when comparing two ratios. We’ll explore whether given ratios are proportional by checking their cross products. Through practical examples, such as balancing weights on a seesaw and mixing ingredients, we will discover how to set up ratios, compute cross products, and solve for unknowns. By the end, you will confidently determine the correctness of ratios and solve proportion-related problems.

kerri
Télécharger la présentation

Understanding Proportions and Cross Products in Ratios

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Solving Proportions Objective: Learn to solve proportions.

  2. Cross Product What is cross product? Cross product is the product (multiplication) of numbers on the diagonal when comparing two ratios. Example: Cross Multiply

  3. More Cross Product Helpful Hint: The cross product represents the numerator of the fraction when a common denominator is found by multiplying the denominators.

  4. Try This! Tell whether the ratios are proportional. Find the cross product Since the cross products are not equal, the ratios are not proportional.

  5. Try This! A mixture for a certain brand of tea should be 3 parts tea to 1 part sugar. If you combine 4 tablespoons of sugar with 12 tablespoons of tea, will the mixture be correct? Set up ratios Find cross products The ratios are equal. The mixture will be correct.

  6. Try This! Find cross products Solve the proportion. Solve for x

  7. Haley weighs 55 lbs and sits on a seesaw 4 ft away from its center. If Josh sits 5ft away from the center and the seesaw is balanced, how much does Josh weigh( j )? ? H J Physical Science Application 4 5 Set up the proportion Find cross product Josh weighs 44 lb.

  8. Example 1: Tell whether the ratios are proportional.

  9. Example 2: Solve each proportion.

  10. Example 3: Allyson weighs 95 lbs and sits on a seesaw 3 ft away from its center. If Marco sits 8 ft away from the center and the seesaw is balanced, how much does Marco weigh?

More Related