1 / 18

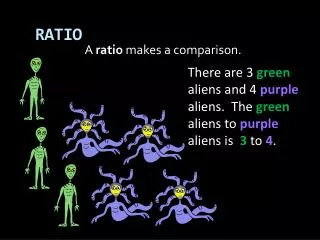
RATIO

RATIO. 7 5. A ratio is a comparison of two quantities. Ratios can be written in several ways. 7 to 5, 7:5, and name the same ratio. 15 ÷ 3 9 ÷ 3. bikes skateboards. Additional Example 1: Writing Ratios in Simplest Form. Write the ratio 15 bikes to 9 skateboards in simplest form.

leala
Télécharger la présentation

RATIO

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. RATIO

  2. 7 5 A ratio is a comparison of two quantities. Ratios can be written in several ways. 7 to 5, 7:5, and name the same ratio.

  3. 15 ÷ 3 9 ÷ 3 bikes skateboards Additional Example 1: Writing Ratios in Simplest Form Write the ratio 15 bikes to 9 skateboards in simplest form. 15 9 Write the ratio as a fraction. = 5 3 Simplify. = = 5 3 The ratio of bikes to skateboards is , 5:3, or 5 to 3.

  4. shirts jeans 24 ÷ 3 9 ÷ 3 Check It Out! Example 1 Write the ratio 24 shirts to 9 jeans in simplest form. Write the ratio as a fraction. 24 9 = 8 3 Simplify. = = 8 3 The ratio of shirts to jeans is , 8:3, or 8 to 3.

  5. When simplifying ratios based on measurements, write the quantities with the same units, if possible.

  6. 3 yards 12 feet 9 ÷ 3 12 ÷ 3 = = = 3 4 3 4 The ratio is , 3:4, or 3 to 4. Additional Example 2: Writing Ratios Based on Measurement Write the ratio 3 yards to 12 feet in simplest form. First convert yards to feet. 3 yards = 3 ● 3 feet There are 3 feet in each yard. Multiply. = 9 feet Now write the ratio. 9 feet 12 feet Simplify.

  7. 36 inches 4 feet 36 ÷ 12 48 ÷ 12 = = = 3 4 3 4 The ratio is , 3:4, or 3 to 4. Check It Out! Example 2 Write the ratio 36 inches to 4 feet in simplest form. First convert feet to inches. 4 feet = 4 ● 12 inches There are 12 inches in each foot. = 48 inches Multiply. Now write the ratio. 36 inches 48 inches Simplify.

  8. Ratios that make the same comparison are equivalent ratios. Equivalent ratios represent the same point on the number line. To check whether two ratios are equivalent, you can write both in simplest form.

  9. 1 9 1 9 12 15 3 27 27 36 2 18 Since , the ratios are equivalent. B. A. = and and 2 18 3 27 2 ÷ 2 18 ÷ 2 3 ÷ 3 27 ÷ 3 = = = = 4 5 3 4 Since , the ratios are not equivalent.  12 15 27 36 12 ÷ 3 15 ÷ 3 27 ÷ 9 36 ÷ 9 = = = = Additional Example 3: Determining Whether Two Ratios Are Equivalent Simplify to tell whether the ratios are equivalent. 1 9 1 9 4 5 3 4

  10. 1 5 1 5 14 49 3 15 9 45 16 36 Since , the ratios are equivalent. A. B. = and and 3 15 9 45 3 ÷ 3 15 ÷ 3 9 ÷ 9 45 ÷ 9 = = = = 2 7 4 9 Since , the ratios are not equivalent.  14 49 16 36 16 ÷ 4 36 ÷ 4 14 ÷ 7 49 ÷ 7 = = = = Check It Out! Example 3 Simplify to tell whether the ratios are equivalent. 1 5 1 5 2 7 4 9

  11. Since , 210 cubic feet of water would have the same mass at 4°C as 20 cubic feet of silver. ft3 silver ft3 water 4 42 20 210 ? ? = = 4 ÷ 2 42 ÷ 2 20 ÷ 10 210 ÷ 10 2 21 2 21 2 21 2 21 = = Additional Example 4: Earth Science Application At 4°C, four cubic feet of silver has the same mass as 42 cubic feet of water. At 4°C, would 20 cubic feet of silver have the same mass as 210 cubic feet of water? Divide. Simplify.

  12. Since , 105 cubic feet of water would have the same mass at 4°C as 10 cubic feet of silver. ft3 silver ft3 water 2 21 10 105 ? ? = = 2 21 10 ÷ 5 105 ÷ 5 2 21 2 21 2 21 2 21 = = Check It Out! Example 4 At 4°C, two cubic feet of silver has the same mass as 21 cubic feet of water. At 4°C, would 105 cubic feet of water have the same mass as 10 cubic feet of silver? Divide. Simplify.

  13. COMPARISON BETWEEN RATIOS AND RATE

More Related