1 / 14

Stability Analysis and Linearization of Incoherent Feed-Forward Loops in Dynamics Systems

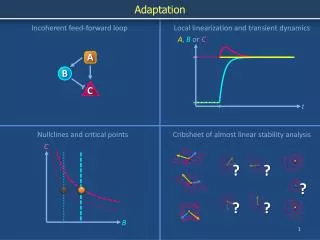
This paper presents a comprehensive cribsheet for analyzing the stability of incoherent feed-forward loops involving multiple variables (A, B, and C). It discusses concepts like local linearization, transient dynamics, nullclines, and critical points, providing examples of parameter ranges and localizations. Key insights include how adaptation influences system behavior and the relationship between variable interdependence and system stability. The analysis includes various mathematical approaches that simplify understanding complex dynamics, essential for designing robust control systems.

leone
Télécharger la présentation

Stability Analysis and Linearization of Incoherent Feed-Forward Loops in Dynamics Systems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Adaptation A, BorC Incoherent feed-forward loop Local linearization and transient dynamics C A B C Nullclines and critical points Cribsheet of almost linear stability analysis ? ? ? ? ? t B

  2. Incoherent feed forward loop -1 +1 A +1 -1 b EB EF a b’ B B c’ C C C g d

  3. Incoherent feed forward loop -1 +1 A 1 1 b EB EF Parameter ranges: 0, << 1, ~1, >>1 a b’ B B c’ C C C 1 1 1/2 g d

  4. Incoherent feed forward loop Input A b EB EF a b’ B B c’ C C C Inhibitory Activating g d Output

  5. Nullclines and critical points E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 1.0 CC at A = 1 is the sameas CC at A = 1/2 owing to compensatory changes in the effects of A and B on C 0.5 STOP B 0 0.5 1.0 1.5 2.0

  6. Adaptation A, BorC Incoherent feed-forward loop Local linearization and transient dynamics C A B C Nullclines and critical points Cribsheet of almost linear stability analysis ? ? ? ? ? t B

  7. Local linearizations E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 DC 1.0 0.5 0.5 B DB 0 0.5 0.5 1.0 1.5 2.0

  8. Local linearizations E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 Squared terms 1.0 0.5 B 0 0.5 1.0 1.5 2.0

  9. Local linearizations E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 1.0 If A = 1/2, 0.5 B 0 0.5 1.0 1.5 2.0

  10. Local linearizations E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 1.0 If A = 1/2, If A = 1, 0.5 B 0 0.5 1.0 1.5 2.0

  11. Putting it together E.g. A = 1/2 C E.g. A = 1 A 2.0 B C 1.5 1.0 0.5 B 0 0.5 1.0 1.5 2.0

  12. Putting it together E.g. A = 1/2 A, BorC C E.g. A = 1 A A Transient 1.1 2.0 1.0 Before B B Late C C 0.9 A= 1/2 1.5 0.8 A= 1 0.7 1.0 0.6 0.5 0.5 0 10 -5 5 15 B t 0 0.5 1.0 1.5 2.0

  13. Adaptation A, BorC Incoherent feed-forward loop Local linearization and transient dynamics C A B C Nullclines and critical points Cribsheet of almost linear stability analysis ? ? ? ? ? t B

  14. The big cribsheet of almost linear stability analysis Node Star Degenerate node Spiral Check shape ? ? Node Center Check stability ? Star Degenerate node Spiral Saddle Check shape ? ?

More Related