1 / 10

EXAMPLE 1

EXAMPLE 1. Identify quadrilaterals. Quadrilateral ABCD has at least one pair of opposite angles congruent. What types of quadrilaterals meet this condition?. SOLUTION. There are many possibilities.

luna
Télécharger la présentation

EXAMPLE 1

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

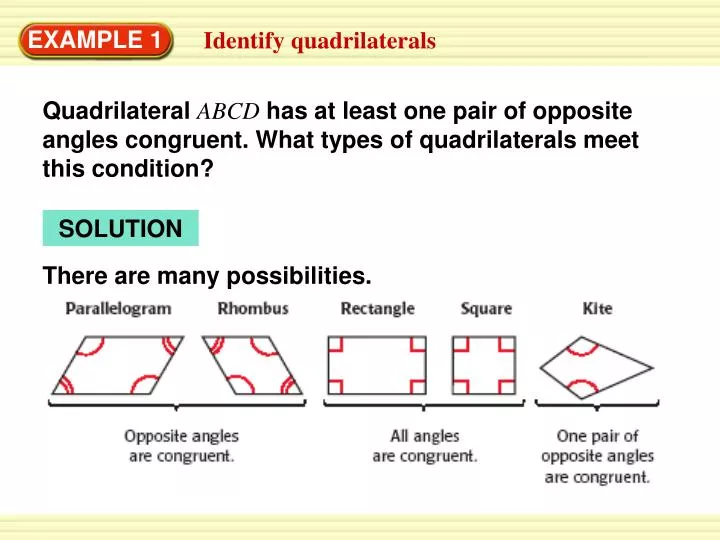
  1. EXAMPLE 1 Identify quadrilaterals Quadrilateral ABCDhas at least one pair of opposite angles congruent. What types of quadrilaterals meet this condition? SOLUTION There are many possibilities.

  2. The diagram shows AE CEand BE DE. So, the diagonals bisect each other. By Theorem 8.10, ABCD is a parallelogram. EXAMPLE 2 Standardized Test Practice SOLUTION

  3. The correct answer is A. ANSWER EXAMPLE 2 Standardized Test Practice Rectangles, rhombuses and squares are also parallelograms. However, there is no information given about the side lengths or angle measures of ABCD. So, you cannot determine whether it is a rectangle, a rhombus, or a square.

  4. Is enough information given in the diagram to show that quadrilateral PQRSis an isosceles trapezoid? Explain. STEP 1 Show that PQRSis a trapezoid. Rand Sare supplementary, but P and S are not. So, PS QR , but PQis not parallel to SR. By definition, PQRSis a trapezoid. EXAMPLE 3 Identify a quadrilateral SOLUTION

  5. STEP 2 Show that trapezoid PQRS is isosceles. P and Sare a pair of congruent base angles. So, PQRSis an isosceles trapezoid by Theorem 8.15. ANSWER Yes, the diagram is sufficient to show that PQRS is an isosceles trapezoid. EXAMPLE 3 Identify a quadrilateral

  6. ANSWER Parallelogram, Rectangle, Square, Rhombus, Trapezoid. for Examples 1, 2, and 3 GUIDED PRACTICE 1. Quadrilateral DEFGhas at least one pair of opposite sides congruent. What types of quadrilaterals meet this condition?

  7. ANSWER Kite: there are two pairs of consecutive congruent sides. for Examples 1, 2, and 3 GUIDED PRACTICE Give the most specific name for the quadrilateral.Explain your reasoning.

  8. ANSWER Trapezoid: there is one pair of parallel sides. for Examples 1, 2, and 3 GUIDED PRACTICE Give the most specific name for the quadrilateral.Explain your reasoning.

  9. ANSWER Quadrilateral; there is not enough information to be more specific. for Examples 1, 2, and 3 GUIDED PRACTICE Give the most specific name for the quadrilateral.Explain your reasoning.

  10. 5. Error Analysis:A student knows the following information about quadrilateral MNPQ:MN PQ ,MP NQ , andP Q. The student concludes that MNPQis an isosceles trapezoid. Explain why the student cannot make this conclusion. ANSWER It’s possible that MNPQ could be a rectangle or a square since you don’t know the relationship between MQ and NP. for Examples 1, 2, and 3 GUIDED PRACTICE

More Related