1 / 32

COMP541 State Machines

COMP541 State Machines. Montek Singh Feb 8, 2012. Today ’ s Topics. State Machines How to design machines that go through a sequence of events “ sequential machines ” Basically close the feedback loop in this picture:. Synchronous Sequential Logic.

michel
Télécharger la présentation

COMP541 State Machines

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. COMP541State Machines Montek Singh Feb 8, 2012

  2. Today’s Topics • State Machines • How to design machines that go through a sequence of events • “sequential machines” • Basically close the feedback loop in this picture:

  3. Synchronous Sequential Logic • Flip-flops/registers contain the system’s state • state changes only at clock edge • so system is synchronized to the clock • all flip-flops receive the same clock signal (important!) • every cyclic path must contain a flip-flop

  4. Two common types • Two common synchronous sequential circuits: • Finite State Machines (FSMs) • Pipelines

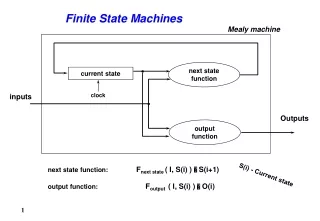
  5. Finite State Machine (FSM) • Consists of: • State register that • holds the current state • updates it to the “next state” at clock edge • Combinational logic (CL) that • computes the next state • using current state and inputs • computes the outputs • using current state (and maybe inputs)

  6. More and Mealy FSMs • Two types of finite state machines differ in the output logic: • Moore FSM: • outputs depend only on the current state • Mealy FSM: • outputs depend on the current state and the inputs • can convert from one form to the other • Mealy is more general • In Both: • Next state is determined by current state and inputs

  7. Moore and Mealy FSMs

  8. FSM Example • Traffic light controller • Traffic sensors: TA, TB (TRUE when there’s traffic) • Lights: LA, LB

  9. FSM Black Box • Inputs: • CLK, Reset, TA, TB • Outputs: LA, LB

  10. Design Simple FSM • When reset, LA is green and LB is red • As long as traffic on Academic (TA high), keep LA green • When TA goes low, sequence to traffic on Bravado • Follow same algorithm for Bravado • Let’s say clock period is 5 sec (time for yellow light)

  11. States • What sequence do the traffic lights follow? • Reset  State 0, LA is green and LB is red • Next (on board)?

  12. State Transition Diagram • Moore FSM: outputs labeled in each state • States: Circles • Transitions: Arcs

  13. State Transition Table

  14. FSM Encoded State Transition Table

  15. FSM Output Table

  16. FSM Schematic: State Register

  17. Next State Logic

  18. Output Logic

  19. FSM Timing Diagram: Study carefully!

  20. Design Procedure • Take problem description and refine it into a state table or diagram • Assign codes to the states • Derive Boolean equations and implement • Or, write Verilog and compile

  21. Example: Sequence Recognizer • Circuit has input, X, and output, Z • Recognizes sequence 1101 on X • Specifically, if X has been 110 and next bit is 1, make Z high

  22. How to Design States • States remember past history • Clearly must remember we’ve seen 110 when next 1 comes along • Tell me one necessary state for this example…?

  23. Beginning State • Start state: let’s call it A • if 1 appears on input, move to next state B • output remains at 0 Input / Output

  24. Second 1 • New state, C • To reach C, must have seen 11

  25. Next a 0 • If 110 has been received, go to D • Next 1 will generate a 1 on output Z

  26. What else? • What happens to arrow on right? • Must go to some state. • Where?

  27. What Sequence? • Here we have to interpret the problem statement • We’ve just seen 01 • Is this beginning of new 1101? • Or do we need to start over w/ another 1? • Textbook: decides that it’s beginning (01…)

  28. Cover every possibility • Well, must have every possibility out of every state • In this case, just two: X = 0 or 1 • You fill in other cases

  29. Fill in

  30. Full Answer

  31. State Minimization • When we make state diagram, do we need all those states? • Some may be redundant • State minimization procedures can be used • Is a tough problem (NP-complete) • but pretty good algorithms exist • exact and approximate • We won’t cover in this course

  32. Reading • Read 3.4-3.6 • Might be good to look at Chapter 4 (Verilog only)

More Related