1 / 4

Understanding Double Integrals and Volume Calculation in a Rectangular Region

This text explores the concept of double integrals and their application in calculating the volume under a function ( f(x, y) ) over a specified rectangular region ( R ) in the xy-plane. It details the partitioning of the rectangle to form sub-rectangles, establishing minimum and maximum values of the function within each sub-rectangle. The relationship between the area of sub-rectangles and the volume under the function is emphasized, particularly in the context of integrable functions and examples illustrating these principles.

nardo
Télécharger la présentation

Understanding Double Integrals and Volume Calculation in a Rectangular Region

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

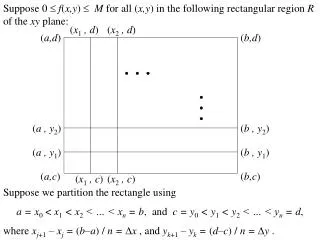
  1. Suppose 0 f(x,y)  M for all (x,y) in the following rectangular region R of the xy plane: (x1 , d) (x2 , d) (a,d) (b,d) (a , y2) (b , y2) (a , y1) (b , y1) (a,c) (b,c) (x1 , c) (x2 , c) Suppose we partition the rectangle using a = x0 < x1 < x2 < … < xn = b, and c = y0< y1 < y2 < … < yn = d, where xj+1 – xj = (b–a) / n=x , and yk+1 – yk = (d–c) / n=y .

  2. We let Rjk be the sub-rectangle [xj , xj+1][yk , yk+1], and we let mjk and Mjk respectively be minimum and maximum values of f on the sub-rectangle. Then, x y = A is the area of each sub-rectangle, and if we let Vjk be the volume under f(x,y) over the sub-rectangle Rjk , then mjkA  Vjk  MjkA . If we let V be the volume under f(x,y) over the rectangle R , then n–1 n–1 n–1 n–1   mjkA  V    MjkA . j=0 k=0 j=0 k=0 If the limit as n exists (and equals V) for both double sums (which will be true for continuous functions), then we say that f is integrable over R; the volume V is f(x,y) dx dy = f(x,y) dA . RR

  3. Example If R is a plate defined by 1 x  2 and 0  y  1 measured in centimeters, and the mass density is described by f(x,y) = yexy , integrate f over R to find the mass of the plate. 1 2 yexydx dy =yexydx dy = R 0 1 1 2 exydy = x=1 0 1 1 (e2y – ey) dy = e2y/2 – ey = e2/2 – e + 1/2 y = 0 0

  4. If f(x,y) is a bounded function on rectangle R (i.e., |f(x,y)| M) and is continuous except possibly for discontinuities along a finite number of continuous curves, then f is integrable on R. See Figure 5.2.4 (page 330). Consider the properties of the double integral stated on page 331. Example 3 on page 338 illustrates a double integral where f(x,y) is not always positive.

More Related