§ 2.2 函数的极限
230 likes | 382 Vues
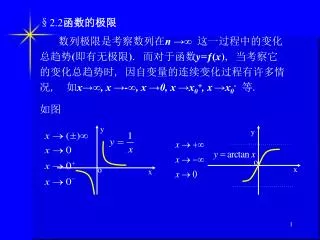
§ 2.2 函数的极限. 数列极限是考察数列在 n →∞ 这一过程中的变化总趋势 ( 即有无极限 ) . 而对于函数 y =ƒ( x ) , 当考察它的变化总趋势时 , 因自变量的连续变化过程有许多情况 , 如 x→∞, x →-∞, x →0, x →x 0 + , x →x 0 - 等. 如图. y. y. o. o. x. x. y. o. x. o. x. 由以上几例可看得出 , 同一个函数的自变量在不同的变化过程中 , 相应的函数变化趋势不一样 , 因而有必要分情况考察. 一 · x → +∞ 时函数 ƒ( x ) 的极限.

§ 2.2 函数的极限
E N D
Presentation Transcript
§2.2函数的极限 数列极限是考察数列在n →∞这一过程中的变化总趋势(即有无极限). 而对于函数y=ƒ(x), 当考察它的变化总趋势时, 因自变量的连续变化过程有许多情况, 如x→∞, x →-∞, x →0, x →x0+, x→x0-等. 如图 y y o o x x
y o x o x 由以上几例可看得出, 同一个函数的自变量在不同的变化过程中, 相应的函数变化趋势不一样, 因而有必要分情况考察. 一· x →+∞ 时函数ƒ(x)的极限 1.直观描述:对函数ƒ(x),当x取正值无限增大时(即x →+∞), 如果ƒ(x)无限接近某常数A, 则称A是函数ƒ(x)当 x →+∞ 时的极限.
由以上几例可看得出, 同一个函数的自变量在不同的变化过程中, 相应的函数变化趋势不一样, 因而有必要分情况考察. 一· x→∞时函数ƒ(x)的极限 1·直观描述:对函数ƒ(x),当x取正值无限增大时(即x→∞ ), 如果ƒ(x)无限接近某常数A, 则称A是函数ƒ(x)当x→∞时的极限. 结论1. 函数 y=1/x, y=arctan x, y=e-x当 x→∞ 时, 以某个确定的常数为极限.而 y=ln x, y=ex, y=logax却不会与常数任意接近.
注:函数y =ƒ(x)当 x→∞时有极限与数列极限的不同点在于自变量一个是连续递增的, 一个是取自然数递增的(是函数极限的特殊情形). 仿数列“ε—N”定义有 2.函数(“ε—M”)定义 设函数ƒ(x),当x>a时有定义.对 使得当x>M时,|ƒ(x)–A|< ε恒成立. 则称函数ƒ(x)当 x→∞时以A为极限.记 则有
几何意义 y 可作两条直线y=A–ε y=ƒ(x) 及y =A+ε.则总存在区间(M,+∞) , A 当 时,对应的函数曲 A+ε 线介于这两条直线之间 o M x 考虑 A–ε 当 x→∞ 时, 以什么为极限?极限是否存在?
3.直观描述: 对函数 ƒ(x),当x取负值而绝对值无限增大时(即x→-∞),如果ƒ(x)无限接近某常数A, 则称A是函数ƒ(x)当x→-∞ 时的极限. 4.函数 (“ε—M”)定义 设函数ƒ(x),当x<–a时有定义. 使得当x<–M时,|ƒ(x)–A|< ε 恒成立.则称函数ƒ(x)当x→-∞ 时以A为极限. y 则有 y=ƒ(x) A+ε A x o 几何意义如右图. –M A–ε
问题:如果既有 又有 是否有 呢? 定理1.函数y =ƒ(x)当x→∞时极限存在且为A的充要条件是函数y =ƒ(x)当 x→+∞ 与 x→-∞ 时极限都存在且等于A. 即 5.精确定义(“ε—M”)设函数ƒ(x),当|x|>a时有定义. 对 使得当|x|>M时, |ƒ(x)–A|< ε恒 成立. 则称函数ƒ(x)当 x→∞时以A为极限. 记为
几何意义如右图. y A+ε y=ƒ(x) A o –M M x A–ε 例3用“ε—M”定义证明
二. x→x0时函数ƒ(x)的极限 y • (1,1) y = x • 1 例4函数 y =ƒ(x) = x(如右图) 当x从大于1和小于1的方向趋于1即当 x→ 1时,函数ƒ(x)无限接近于1, 记为 f(x)→1 • x o 1 由前知 , ƒ(x)与1的接近程度可由|ƒ(x)–1|< ε 来刻划; 那么x与1的接近又怎样来刻划呢? 由|ƒ(x)–1|= |x–1|知,要使 |ƒ(x)–1|< ε, 只须 |x–1|<ε即可. 显然,此时可表示x与1的无限接近了, 即ε可刻划 x 与1的接近程度.若记δ = ε >0,则有“ 当 x→1时,f(x)→1 ”的精确描述:
1.精确定义(“ε—δ”) 函数ƒ(x), 在x0的某邻域内(可去心)有定义. 恒有| ƒ(x) – A |< ε成立. 则称函数ƒ(x)当 x→x0时以A为极限.记为 从而
几何意义 可作两条直线 y = A–ε及 y = A+ε. 则在x轴上总存在以 x0为心, δ为半径的去心 邻域 即在该去心邻域内对应的函数曲线一步y=f(x)介于这两条直线之间, 如下图. y A+ε y=ƒ(x) º A A–ε ° o x
例4用“ε—δ”定义证明(关键由|ƒ(x)–A|< ε解出0<|x-x0|<g(ε), 得到δ )
例4的(3)的证明 无定义,则当 x≠1时, 由于当x=1时 要使|ƒ(x)–A|< ε 即 只须 即可.故可取δ= ε/2. 恒有 成立.即
注:此例中函数虽在x=1处无定义,但 x→1时极限 却存在.这说明函数在 x0点的极限是否存在与函数 在 x0处有无定义无关.这是因为函数在 x0点的极限 是函数在 x0附近的变化趋势, 而不是在 x0处函数 值.这就是在定义中为啥假设ƒ(x)可在 x0处无定义 的原因了.
三. 函数ƒ(x)的左、右极限 如 则只能考察 x 从 0 的右侧趋于 0 时的极限. 因而必须引进左、右极限的概念. 中所讨论的x→x0即x可从 x0的左右 两侧趋于x0. 但有时可考察 x仅从x0的左侧或右侧趋近时函数(特别是分段函数在分段点处)的极限. 1.左极限的直观描述及精确定义(“ε—δ”) 当x从 x0左侧(小于)趋于x0时 , ƒ(x)以A为极限. 则 A是ƒ(x)在 x0处的左极限. 记为 “ε—δ”定义
2.右极限的直观描述及精确定义(“ε—δ”) 当x从 x0右侧(大于)趋于x0时 , ƒ(x)以A为极限. 则 A是ƒ(x)在 x0处的右极限. 记为 “ε—δ”定义 注: 左极限和右极限统称为单侧极限. 它们之间有如下关系: 定理2.函数y = ƒ(x)当 x→x0时极限存在且为A的充要条件是函数y = ƒ(x)的左极限和右极限都存在且等于A. 即
此定理给出了怎样利用单侧极限判断函数极限存在的方法; 特别对分段函数适用. 例5.设ƒ(x)=|x| ,求 解 因 则 y y =|x| • o x 故 讨论下列函数当 x→0 时的极限.
例6. y= [x]在 x→1时极限是否存在? y 解 因 • ° • ° x o 故 1 例7. 解 因
例8. 解 因 由于左右极限存在但不相等, 所以 f (x)的极限 不存在.
四.函数极限的几个重要性质 为了叙述方便, 将ƒ(x)在 x→∞或 x→x0 时的极限 A 统一表述为: 对 总存在那么一个时刻, 在此 时刻以后, 就恒有| ƒ(x) – A |< ε,并记为 lim ƒ(x) = A 定理3.(唯一性) 若lim ƒ(x) = A存在, 则极限值 A 唯一. 其证明同§2.1的性质1.(略) 注: 若不唯一, 变化趋势不定. 例
定理4.(有界性) 若 lim ƒ(x) = A存在, 则一定存在那么一个时刻, 在此时刻以后, ƒ(x)必定有界. 其理论证明(略).直观地可由几何意义(介于A–ε及 y =A+ε之间)说明.