1 / 50

Enhancing Robust Sender Anonymity in Communication Protocols: A Case Study of DC-Nets

This work in progress examines robust sender anonymity properties in communication protocols, focusing on the DC-Nets system. We investigate various anonymity properties, including sender anonymity, receiver anonymity, and unlinkability both for senders and receivers. The protocol aims to maintain anonymity even in the presence of active adversaries. The research defines robust anonymous protocols that protect participant identities, ensuring honest messages are delivered despite potential corrupt participants. We provide foundational analysis and insights into robustness and its implications for privacy in digital communications.

qabil
Télécharger la présentation

Enhancing Robust Sender Anonymity in Communication Protocols: A Case Study of DC-Nets

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Robust Sender AnonymityTamara Rezk FMCrypto (work in progress) G.Barthe, A.Hevia, Z.Luo, T.Rezk, B.Warinschi April, 28th – Campinas, Brazil

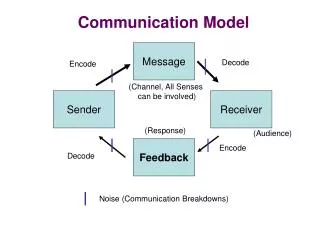
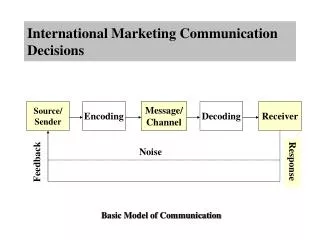
  2. Anonymity Protocols • Hide the identity associated to a message • The message may be public. Example:voting • Different kind of anonymity properties

  3. Anonymity Properties • Receiver anonymity • Sender Unlinkability (SUL) • Receiver Unlinkability (RUL) • Sender-Receiver Unlinkability (UL) • Sender Anonymity (SA) • Strong Sender Anonymity (SA*) • Receiver Anonymity (RA) • Strong Receiver Anonymity (RA*) • Sender-Receiver Anonymity (SRA) • Unobservability (UO) • Sender Unlinkability (SUL) • Receiver Unlinkability (RUL) • Sender-Receiver Unlinkability (UL) • Sender Anonymity (SA) • Strong Sender Anonymity (SA*) • Receiver Anonymity (RA) • Strong Receiver Anonymity (RA*) • Sender-Receiver Anonymity (SRA) • Unobservability (UO)

  4. 7 Anonymity Properties Characterizations [Micciancio&Hevia06] 1 2 3 4 5 6 7 8 a 1 5 a 1 b 2 b 6 2 a 3 a 7 3 c 4 c d 8 4 d M = 5 6 7 8 mij = sets of messages from party i to party j (Thanks Alejandro for this slide)

  5. = multiset c d for each row i d c M0 M1 Capturing information leaks • By restricting the matrix pair M0,M1 • Let f(M) be the information leaked • Requirement: f(M0) = f(M1) • Example of leaked information: (Thanks Alejandro for this slide)

  6. The anonymity property for protocol PHypothesis: f(M0) = f(M1) CA:=b := {0,1}; if (b = 0) then {m := M0} else {m := M1}; S  P(m) g A(S,f(m)) | Pr[CA; g = b] - ½ | is negligible on the security parameter

  7. Motivation • Anonymity in the case of active adversaries • Case study: DC-Nets

  8. Motivation • Anonymity in the case of active adversaries • Case study: DC-Nets • Robustness was not what we expected it to be • Work: definition of robustness

  9. Robust anonymous protocol • A protocol that is anonymous (it does not leak the identity of the participants)

  10. Robust anonymous protocol • A protocol that is anonymous even if some of the participants are corrupt

  11. Robust anonymous protocol • A protocol that is anonymous even if some of the participants are corrupt • Honest messages can be delivered even if dishonest participants do not follow the protocol

  12. Robust anonymous protocol • Anonymity property for active adversaries • Robustness property

  13. The anonymity property for protocol Pfor active adversariesHypothesis: f(M0) = f(M1) CRA:=b := {0,1}; if (b = 0) then {m := M0} else {m := M1}; gA[P(m)] (f(m)) | Pr[CRA; g = b] - ½ | is negligible on the security parameter

  14. Dinning Cryptographers:all started in a restaurant …

  15. Dinning Cryptographers Protocol (DC-nets) • Bitwise XOR [Chaum88] • Not robust • Bilinear Maps [GolleJuels04] • Robust What does exactly the word “robust” assure?

  16. The robust DC-nets protocol 1/4 inizialization • In this phase: • a non-degenerate pairing e : G1 x G1  G2 • generators g, h of a cyclic group G1 • a hash function H: {0,1}*  G1 • a private key xi and public key yi = g^xi (secret xi is (t,n)-shared ) • a common reference string

  17. The robust DC-nets protocol 2/4 inizialization transmission In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding.

  18. transmission 1/3 In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding. 1 2 i n

  19. transmission 2/3 In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding. 1 • e(H(s||2), yj)^xi*c • ji 2 i n

  20. transmission 3/3 In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding. 1 • e(H(s||2), yj)^xi*c • ji 2 Padding participant i. Coefficient c is 1 if i<j or -1 otherwise. i n

  21. transmission 3/3 In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding. • e(H(s||2), yj)^xi*c • ji • * • m 1 2 i Message m transmission n

  22. transmission If each participant transmits exactly one message without collisions then multiplication of vectors yields the messages. Vector Party 1 Vector Party n 1 1 1 1 m1 m2 … mn 2 2 2 2 = * * … n n n n

  23. transmission Example for 2 paticipants: n=2 1/9

  24. transmission Example for 2 paticipants: n=2 2/9 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 1 2 Vector Party 1

  25. transmission Example for 2 paticipants: n=2 3/9 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 1 1 2 2 Vector Party 1 Vector Party 2

  26. transmission Example for 2 paticipants: n=2 4/9 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  27. transmission Example for 2 paticipants: n=2 5/9 e(H(s||1), y2)^x1 * e(H(s||1), y1)^-x2 * m1 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  28. transmission Example for 2 paticipants: n=2 6/9 e(H(s||1), y2)^x1 * e(H(s||1), y1)^-x2 * m1 = {public key inlining} e(H(s||1), x2g)^x1 * e(H(s||1), x1g)^-x2 * m1 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  29. transmission Example for 2 paticipants: n=2 7/9 e(H(s||1), y2)^x1 * e(H(s||1), y1)^-x2 * m1 = {public key inlining} e(H(s||1), x2g)^x1 * e(H(s||1), x1g)^-x2 * m1 = {bilinearity} e(H(s||1), x1x2g) * e(H(s||1), x2x1g)^-1 * m1 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  30. transmission Example for 2 paticipants: n=2 8/9 e(H(s||1), y2)^x1 * e(H(s||1), y1)^-x2 * m1 = {public key inlining} e(H(s||1), x2g)^x1 * e(H(s||1), x1g)^-x2 * m1 = {bilinearity} e(H(s||1), x1x2g) * e(H(s||1), x2x1g)^-1 * m1 = {conmutativity} e(H(s||1), x1x2g) * e(H(s||1), x1x2g)^-1 * m1 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  31. transmission Example for 2 paticipants: n=2 9/9 e(H(s||1), y2)^x1 * e(H(s||1), y1)^-x2 * m1 = {public key inlining} e(H(s||1), x2g)^x1 * e(H(s||1), x1g)^-x2 * m1 = {bilinearity} e(H(s||1), x1x2g) * e(H(s||1), x2x1g)^-1 * m1 = {conmutativity} e(H(s||1), x1x2g) * e(H(s||1), x1x2g)^-1 * m1 ={inverse *} m1 e(H(s||1), y2)^x1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 m1 m2 1 1 1 = * 2 2 2 Vector Party 1 Vector Party 2 transmission result

  32. transmission If there is a collision, or the padding is incorrect, or there is more than one message in the vector, recuperation of messages fail! Vector Party 1 Vector Party n 1 1 1 1 m1 m2 … mn 2 2 2 2 = * * … n n n n

  33. transmission Vectors are transmitted with a proof of knowledge (zkpk) For all positions in the vector there is a valid padding, except for at most one position.

  34. The robust DC-nets protocol 3/4 inizialization transmission reconstruction In this phase: each participant computes a vector that contains a “padding” and a unique message that cannot be distinguished from the padding.

  35. reconstruction In this phase: if a proof of knowledge does not verify then the vector of the dishonest participant is reconstructed using trheshold cryptography After this phase, we are left with a set of valid vectors , that is : For all positions in the vector there is a valid padding, except for at most one position.

  36. The robust DC-nets protocol 4/4 inizialization transmission reconstruction recuperation

  37. recuperation In this phase: All vectors are correct (honest participants or recovered vectors). Messages are recuperated by multiplication. Vector Party 1 Vector Party n 1 1 1 1 m1 m2 … mn 2 2 2 2 = * * … n n n n

  38. What does exactly the word “robust” assure? • If the vector is correct, then there is a unique message in the vector • An adversary may violate the slot reservation protocol to intentionally produce a collision • For each collision, one honest message is not delivered

  39. We propose to state this formally by definning a: Robustness property

  40. Sender robustness, t-n SR:= M,N  A0 m := M++N; SP[A](m) if (#(MПS) < 2t-n) then b’:=1 else b’:=0 |Pr[SR; b’=1] is negligible on the security parameter

  41. Sender Robustness Violation 1 Example for 2 paticipants: n=2 ???? m2 1 = * 2 Vector Party 1 Vector Party 2 transmission result 1 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 1 1 2 2

  42. Sender Robustness Violation 2 Example for 2 paticipants: n=2 ???? m2 1 = * 2 Vector Party 1 Vector Party 2 transmission result e(H(s||2), y2)^x1*m2 e(H(s||2), y2)^x1*m2 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 1 1 2 2

  43. Sender Robustness Example for 2 paticipants: n=2 m1*m2 m2 1 = * 2 Vector Party 1 Vector Party 2 transmission result This is considered secure! e(H(s||2), y2)^x1*m2 e(H(s||2), y2)^x1 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 1 1 2 2

  44. A stronger robustness propertyConfusion resistant t-n CR:= M,N  A0 m := M++N; SP[A(m)] if honest received < honest-dishonest then b’:=1 else b’:=0 |Pr[CR; b’=1] is negligible on the security parameter

  45. A stronger robustness propertyConfusion resistant t-n CR:= M,N  A0 m := M++N; SP[A(m)] if honest not received+dishonest received > dishonest. then b’:=1 else b’:=0 |Pr[CR; b’=1] is negligible on the security parameter

  46. A stronger robustness propertyConfusion resistant t-n CR:= M,N  A0 m := M++N; SP[A(m)] if (#(S\M) + #(M\S) > n-t) then b’:=1 else b’:=0 |Pr[CR; b’=1] is negligible on the security parameter

  47. Confussion Resistant Violation Example for 2 paticipants: n=2 m1*m2 m2 1 = * 2 Vector Party 1 Vector Party 2 transmission result e(H(s||2), y2)^x1*m2 e(H(s||2), y2)^x1 e(H(s||1), y1)^-x2 *m1 e(H(s||2), y1)^-x2 1 1 2 2

  48. Theorems and Remarks • Theo: DC-Nets is sender anonymous • Theo: DC-Nets is sender robust • Remark: DC-Nets is not confussion resistant

  49. Theorems and Remarks • Theo: DC-Nets is sender anonymous • Theo: DC-Nets is sender robust • Remark: DC-Nets is not confussion resistant Solution? : messages should be “sealed” in such a way that multiplication of two seals produces another seal only with negligible probability

  50. Conclusions • We have a proposed 2 properties to formally specify robustness of sender anonymous protocols • We have detected GJ protocol satisfies only a weak form of robustness, and proposed a stronger version of the protocol • Open questions: how to implement the stronger GJ?, how all these definitions extend to other forms of anonymity? generic conversion to stronger robustness?

More Related