Exponential and Logarithmic Functions
510 likes | 831 Vues
Exponential and Logarithmic Functions. Solve, round to nearest hundredth. Answer. Solve, round to nearest hundredth. Answer. Solve, round to nearest hundredth. Answer. Solve, round to nearest hundredth. Answer. Solve, round to nearest hundredth. Answer. Write in logarithm form. Answer.

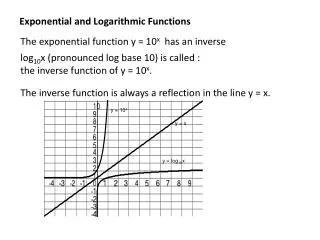
Exponential and Logarithmic Functions
E N D
Presentation Transcript
Write in logarithm form Answer
Write in exponential form Answer
Expand the expression Answer
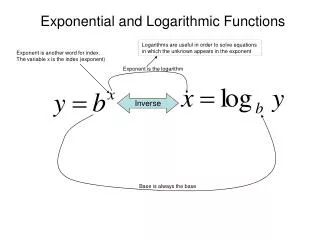
Find the inverse. Answer
Find the inverse. Answer
Find the inverse. Answer
Find the inverse. Answer
Find the inverse. Answer
Suppose you deposit $1500 in a savings account that pays 6%. No money is added or withdrawn form the account. Write an equation to model this situation. How much will the account be worth in 5 years? How many years until the account doubles? Answer
Suppose you deposit $1500 in a savings account that pays 6%. No money is added or withdrawn form the account. Write an equation to model this situation. How much will the account be worth in 5 years? How many years until the account doubles? 12 years
In 2009, there were 1570 bears in a wildlife refuge. In 2010 approximately 1884 bears. If this trend continues and the bear population is increasing exponentially, how many bears will there be in 2018? Write an exponential function to model the situation, then solve. Answer
In 2009, there were 1570 bears in a wildlife refuge. In 2010 approximately 1884 bears. If this trend continues and the bear population is increasing exponentially, how many bears will there be in 2018? Write an exponential function to model the situation, then solve. 8,100 bears
Suppose the population of a country is currently 7.3 million people. Studies show this country’s population is declining at a rate of 2.3% each year. Write an equation to model this situation. How many years until the population goes below 4 million? Answer
Suppose the population of a country is currently 7.3 million people. Studies show this country’s population is declining at a rate of 2.3% each year. Write an equation to model this situation. How many years until the population goes below 4 million? 26 years
By measuring the amount of carbon-14 in an object, a paleontologist can determine its approximate age. The amount of carbon-14 in an object is given by y = ae0.00012t, where a is the amount of carbon-14 originally in the object, and t is the age of the object in years. A fossil of a bone contains 32% of its original carbon-14. What is the approximate age of the bone? Answer
A new truck that sells for $29,000 depreciates 12% each year. What is the value of the truck after 7 years? Answer
Domain: All real numbers Range:
Domain: All real numbers Range:
Domain: Range: All real numbers
Domain: Range: All real numbers