1 / 30

GEOMETRY SOL IDEAS

GEOMETRY SOL IDEAS. Complementary angles have the sum of 90. Angles that form a LINEar pair are supplementary (180). Vertical angles are opposite each other. They are equal. Constructions (Use tracing paper! ) paper ruler, plastic compass 1. Segment / Angle Bisector

rlaird
Télécharger la présentation

GEOMETRY SOL IDEAS

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. GEOMETRY SOL IDEAS

  2. Complementary angles have the sum of 90. Angles that form a LINEar pair are supplementary (180). Vertical angles are opposite each other. They are equal.

  3. Constructions (Use tracing paper!) paper ruler, plastic compass 1. Segment / Angle Bisector 2. Congruent Segments / Angles 3. Perpendicular lines (90 degrees) 4. Perpendicular bisector

  4. ISOSCELES EQUI Venn Diagrams intersection = common no intersection  nothing in common Circle inside another circle “All bulldogs are dogs.”

  5. Conditional (p  q) Converse (q  p) switch Inverse (p q) not-not Contrapositive (q p) Symbolic Representation p: the opposite of p

  6. Parallel Lines (only 2 Options: = or 180) alternate interior angles ( = ) Zorro alternate exterior angles ( = ) corresponding angles ( = ) consecutive interior angles (180)

  7. Parallel lines have EQUAL slopes. Perpendicular lines have ‘opposite reciprocal’ slopes. 2/3 & -3/2 Compute SLOPES visually. from left to right, count rise over run.

  8. Triangle Sum Theorem The sum of the 3 angles is 180. An equilateral triangle is always a 60-60-60 triangle. An equilateral triangle is isosceles. (3 = sides means 2 = sides)

  9. The base angles of an isosceles triangle are congruent. (BAT) Ext. Angle Theorem: out = in + in SAS, SSS, ASA, AAS (no SSA) Use ticks & arcs.

  10. Triangle Inequality Ideas The bigger the angle, the longer the opposite side, & vice-versa. Draw and label a figure! S, M, L or L, M, S Arrange from least to greatest, greatest to least… (be careful!)

  11. Triangle Inequality Theorem sum of 2 shorter sides >3rd side Technique: Add 2 sides, Subtract 2 sides (This gives the possible values for 3rd side.)

  12. Similar triangles: corresponding sides are proportional (EQ:ratio = ratio) S/S = M/M = L/L Corresponding angles are congruent. The sequence of letters is important!

  13. Proportionality Theorems part / part = part / part (for any two SIMILAR figures) ratio of perimeters = scale factor (ratio of sides)

  14. Pythagorean Theorem Pythagorean Triples (5,12,13 ; 7, 24, 25 ; 3, 4, 5 ; etc.) The altitude drawn to the hypotenuse gives rise to THREE similar triangles. (tic-tac-toe)

  15. Special Right Triangles (shortcuts) • 45-45-90 (half-square) • legs are = • a  c: multiply bysq. rt. of 2 • 30-60-90 • a  c: multiply by 2 • a  b: multiply by sq. rt. of 3

  16. Trigonometry [Degree Mode!!] 3 steps: Label the sides. (eyeball) EQ: SOH-CAH-TOA Cross-multiply elevation = depression Zorro

  17. COODies for Parallelograms (Set up equation based on these properties.) Special Properties Diagonals of a rhombus are perpendicular. Diagonals of a rectangle are =.

  18. Transformations or Movements (translation, rotation, reflection) ‘slide’ ‘turn’ ‘flip’ Symmetry Lines for Polygons regular polygons  ‘n’ sides Point Symmetry (hexagon, S, O, N) (when you turn by 180, you get same picture)

  19. Rotation: Center & Angle (connect technique) Reflection: Across Different Axes Translation: sliding an object Images of Points (X, Y, Z  X’, Y’, Z’) Watch out for the correspondence!

  20. Tangents & Ice Cream Cones Tangent line is perpendicular to the radius. Use P.T. Angle-Arc Relationships 1. Central Angle = Opposite Arc 2. Inscribed Angle is ½ of Arc

  21. 180 and 360degree principles Semi-circle = 180 (diameter) Inscribed angle that cuts a semi-circle = 90 (L-shape)

  22. Segment relationships (part)(part) = (part)(part) (out)(total) = (out)(total) tangent squared = (out)(total) Other angle-arc relationships in: (BIG + SMALL) / 2 (x – 2)^2 + (y + 5)^2 = 16 Center: (2, -5) and radius r = 4

  23. Polygon Formulas (MEMORIZE) (n – 2)(180)  sum of interior angles Divide the above by n  measure of EACH interior angle (regular polygons) n  number of sides (also the number of angles)

  24. 360  sum of exterior angles 360 / n  each exterior angle 360 / ext. angle  n (sides) The exterior & interior angles of any polygon add up to 180. (‘extend a side’ technique)

  25. Areas of Similar Polygons (ratio of sides) squared Circumference and Arc Length divide angle by 360 first Areas of Sectors (pizza slice) divide angle by 360 first Then multiply…

  26. 3 dimensional figures (scaling, fitting in a piece, nets) 3 perspective views (top, side, front)  use common sense!

  27. Surface Area and Volume Formulas (5 solids) Use Formula Sheet! B  area of base (8 x 8) h  height l  slant height (use P.T.) r  radius (half of diameter)

  28. Similar Figures / Solids Ratio of Sides = Scale Factor Ratio of Areas (squared/squared) if scale is 2:3, then areas ratio is 4:9 Ratio of Volumes (cubed/cubed) if scale is 2:3, then volumes ratio is 8:27 Some problems don’t require the use of formula sheet. Set up ratio = ratio.

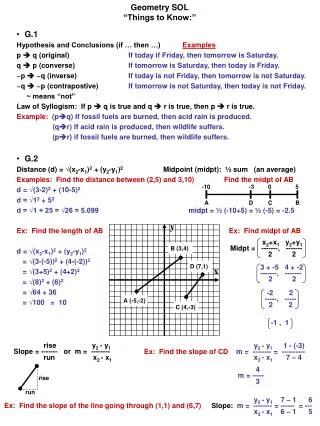
  29. Label points first! (x1,y1) & (x2,y2) Use techniques shown in class. Slope: Distance: Midpoint: add & divide by 2

  30. Good Luck! Give it your best shot! (time incentive)

More Related