1 / 51

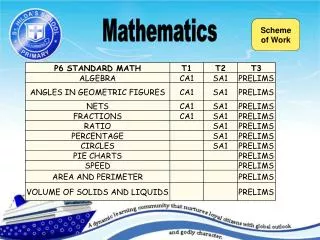
Mathematics

Mathematics. Session. Circle - 1. Session Objectives. Session Objective. 1. Definition -Locus. 2. Different forms of circle. -Standard form -End-point diameter form -General form -Parametric form. 3. Condition for second degree equation to represent a circle. y. x.

sheera
Télécharger la présentation

Mathematics

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Mathematics

  2. Session Circle - 1

  3. Session Objectives

  4. Session Objective 1. Definition -Locus 2. Different forms of circle -Standard form -End-point diameter form -General form -Parametric form 3. Condition for second degree equation to represent a circle

  5. y x Definition-Locus Definition: locus of a point in a plane which is at a fixed given distance from a fixed given point in the plane is circle center radius C(xc,yc)  center; Rradius . P(x,y) R P(x,y)  Any point on the circle C(xc,yc) O(0,0)

  6. Definition-Locus By distance formula (x-xc)2+(y-yc)2=R2 PC2= P(x,y) Locus of any point on the circle This is also called Standard form R C(xc,yc)

  7. P(x,y) . C(h,k) P(x,y) . y P(x,y) C(xc,yc) R C(0,0) x Standard form Standard form of the circle center at C(xc,yc) and radius R (x-xc)2+(y-yc)2=R2 Special Cases: Case1 When origin coincides with center of circle . . . Corresponding equation is called center at origin form x2+y2=r2

  8. Illustrative Problem Find the equation of the circle having center at (3,4) and passes through (6,7) Solution: Find radius Radius=distance of points (3,4) & (6,7)=18 Use Standard form Ans: (x-3)2+(y-4)2=18

  9. P(2,3) x-y=0 r Point of intersection of x-y=0 and 3x-4y+1=0 Center Of Circle 3x-4y+1=0 Equation of circle: (x-1)2+(y-1)2=5 Illustrative Problem Find the equation of the circle having x-y=0 and 3x-4y+1=0 as diameters and passes through (2,3) Solution O (1,1) x-y=0 3x-4y+1=0 By Solving, we get Center(1,1) r2=PO2=(2-1)2+(3-1)2=5

  10. y A(x1,y1) . B(x2,y2) x End-Point Diameter Form Equation of the circle whose end-points of one diameter are given as A(x1,y1) and B(x2,y2) Any points on the circle P(x,y) Slope of AP=(y-y1)/(x-x1) Slope of BP=(y-y2)/(x-x2) APBP O(0,0) (Slope of AP) x (slope of BP)=-1

  11. Any points on the circle y A(x1,y1) P(x,y) . B(x2,y2) x End-Point Diameter Form (y-y1)(y-y2)= - (x-x1)(x-x2) (x-x1)(x-x2)+(y-y1)(y-y2)=0 End-point diameter form of circle O(0,0)

  12. Illustrative Problem Find the centre and radius of the circle represented by (x-x1)(x-x2)+(y-y1)(y-y2)=0 Solution: Two extremities of diameter  P(x1,y1) and Q(x2,y2) Centre is the mid-point of PQ Q(x2,y2) .C Radius=CP=CQ P(x1,y1)

  13. 3x+4y-12=0 (4,0) Illustrative Problem Find the equation of circle of diameter 5 units, passes through (4,0) and has 3x+4y-12=0 as equation of diameter Solution: Observe:(4,0) lies on 3x+4y-12=0 Equation of the line is x=4+r cos  y= 0+r sin  Parametric form of line tan =slope of line=(-3/4)  cos =(-4/5) and sin =(3/5)

  14. Solution Cont. r=  5 and cos =(-4/5) and sin =(3/5) Let the other end of diameter be (x1,y1) x1=4+5 (-4/5)=0 y1=0+ 5 (3/5)=3 for r=5 or x1=4-5 (-4/5) =8 y1= 0-5 (3/5) =-3 for r=-5 Other end of the diameter is either(0,3) or (8,-3)

  15. Solution Cont. 3x+4y-12=0 (0,3) (4,0) (x-0)(x-4)+(y-3)(y-0)=0 (8,-3) or x(x-4)+y(y-3)=0  x2+y2-4x-3y=0 (x-8)(x-4)+(y+3)(y-0)=0 x2+y2-12x+3y+32=0

  16. General Form Standard form: (x-xc)2+(y-yc)2=R2 ………….(1)  x2+y2-2xcx-2ycy+ xc2+ yc2- R2=0 In general formit is written as: x2+y2+2gx+2fy+ c=0 , where g, f, c R Comparing with (1) g=-xc, f=-yc c= xc2+ yc2- R2

  17. General Form x2+y2+2gx+2fy+ c=0 represents circle having center at (-g,-f) general form of circle and radius= 1. g2+f2-c>0 real circle (R>0) ? 2. g2+f2-c=0  Point circle (R=0) 3. g2+f2-c<0  Imaginary circle (R<0) ?

  18. Illustrative Problem Find the centre & radius of the circle 2x2+2y2-6x+6y-5=0 Centre (3,-3)? Solution: Note:- center is (-g,-f) when co-eff of x2 & y2 is 1 Make co-eff of x2 & y2 as 1 x2+y2-3x+3y-(5/2)=0 g=-(3/2); f=3/2;c=-5/2 Centre(3/2,-3/2)

  19. Illustrative Problem Show that the four points (1,0), (2,-7),(8,1) and (9,-6) are concylic. i.e,lie on the same circle. Solution: Let x2+y2+2gx+2fy+c=0 be the equation of the circle. As it passes through (1,0)  2g+c=-1------(i) 12+02+2g.1+2f.0+c=0 As it passes through (2,-7) 22+(-7)2+2g.2+2f.(-7)+c=0  4g-14f+c=-53------(ii) As it passes through (8,1) 82+12+2g.8+2f.1+c=0  16g+2f+c=-65------(iii)

  20. Solution Cont. 2g+c=-1------(i) 4g-14f+c=-53------(ii) 16g+2f+c=-65------(iii) (ii)-(iii)  -12g-16f=12 (ii)-(i)  2g-14f=-52 or, 3g+4f = -3 or, g-7f = -26 By Solving  c=9 g=-5 ,f=3 Equation of the circle is: x2+y2-10x+6y+9=0 For (9,-6) : L.H.S= 92+(-6)2-10.9+6.(-6)+9 = 0 Four points are Concylic

  21. Condition For 2nd Degree Equn to Represent Circle General form of 2nd degree equn:- ax2+by2+2gx+2fy+2hxy+c=0---(1) where a,b,g,f,h,c  R It represents curves of different kind 2gx+2fy+c=0 AS : 1. for a=b=h=0 (and g ,f  0)  equn (1) be straight line

  22. Condition For 2nd Degree Equn to Represent Circle General 2nd degree equation: ax2+by2+2gx+2fy+2hxy+c=0---(i) General equation of the circle :x2+y2+2gx+2fy+c=0-------------(ii) So general 2nd degree equation will represent circle iff 1. Co-eff of x2=Co-eff y2 0  a = b  0 By Comparing (i) and (ii) 2. Co-eff of xy=0  h=0

  23. Illustrative Problem Given that ax2+by2+2gx+2fy+c=0 represents circle. Then find the radius of the circle? Solution: As ax2+by2+2gx+2fy+c=0---(1) represents a circle a=b  0 Equation (1) can be written as

  24. L2=0 L3=0 L1=0 Illustrative problem Find the equation of the circle passes through the point of intersection of lines x+y=6, 2x+y=4 and x+2y=5 Solution: Let L1 x+y-6=0 L2  2x+y-4=0 L3 x+2y-5=0 p3 L1L2+  L1L3+  L3L2=0 p1 What does it represent? p2

  25. Solution Cont. p3 (x3,y3) L3=0 L2=0 L1=0 p1 p2 (x1,y1) (x2,y2) f(x,y)=L1L2+  L1L3+  L3L2 (1) f(x,y)= (x+y-6)(2x+y-4)+(x+y-6)(x+2y-5) +(x+2y-5)(2x+y-4) x1+y1-6=0 and 2x1+y1-4=0 As P1(x1,y1) lies on L1=0 and L2=0 By putting P1(x1,y1) in (1)

  26. p3 (x3,y3) L3=0 L2=0 L1=0 p1 p2 (x1,y1) (x2,y2) Solution Cont. x1+y1-6=0 and 2x1+y1-4=0 f(x1,y1)= (x1+y1-6)(2x1+y1-4)+(x1+y1-6)(x1+2y1-5) +(x1+2y1-5)(2x1+y1-4) = 0x0+ x0x(x1+2y1-5) +(x1+2y1-5)x0 = 0  P1 lies on f(x,y) Similarly it can be proved that P2 and P3 also lies on f(x,y).

  27. p3 (x3,y3) L3=0 L2=0 L1=0 p1 p2 (x1,y1) (x2,y2) Solution Cont. • points of intersections of L1=0, L2=0 and L3=0 lies on curve f(x,y)=0 P1,P2,P3 lies on f(x,y)=0 Represents curve, which passes through the point of intersection of L1=0, L2=0 and L3=0 L1L2+  L1L3+  L3L2=0

  28. Solution Cont. L1L2+  L1L3+  L3L2=0 (x+y-6)(2x+y-4) +(x+y-6) (x+2y-5) +(x+2y-5)(2x+y-4)=0 1.Co-efficient of x2=co-efficient of y2 2++2=1+2+2-------(1) Will represent circle 2.Co-efficient of xy=0 3+3+5=0------------(2) From (1) and (2): =1 ,= -6/5

  29. Solution Cont. L1L2+  L1L3+  L3L2=0 For =1 and =-6/5 the curve represents circle Equation of circle is (x+y-6)(2x+y-4)+(x+y-6)(x+2y-5) -(6/5)(x+2y-5)(2x+y-4)=0 • x2+y2 -17x-19y+50 = 0 is the equation of the circle

  30. P(x,y) R  C(xc,yc) (R sin) yc+Rsin w.r.t x-axis yc xc (R cos) xc+Rcos Parametric Form For the circle (x-xc)2+(y-yc)2=R2 point P(x,y) on circle represented as: x= xc + R cos  . y= yc + R sin  =y collectively represents all the points on circle for different values of : 0  360 =x

  31. y P(x,y) . R R sin  x R cos Parametric Form (x-xc)2+(y-yc)2= R2 Parametric form Special case: For the circle x2+y2=R2 Parametric form:-

  32. Illustrative Problem Find the parametric equation of the circle x2+y2-4x-2y+1=0 Solution: Find the center(h,k) & radius(r) h=2, k=1, r=2 Put in the parametric form x=(2+2cos); y=(1+2 sin )

  33. Class Exercise

  34. 2x-3y+12=0 Point of intersection of x+4y-5=0 and 2x-3y+12=0 Center Of Circle x+4y-5=0 Class Exercise -1 Find the equation of the circle whose diameters are 2x–3y+12=0 and x+4y–5=0 and area is 154 Solution: O (-3,2) 2x-3y+12=0 x+4y-5=0 By Solving, we get Center(-3,2) Let the radius of circle is r. Equation of circle is (x+3)2+(y–2)2=49

  35. Class Exercise - 2 • Find the parametric form of the circle: x2+y2+px+py=0. Solution: • x2+y2+px+py=0. Parametric Form of Equation

  36. Class Exercise - 3 Find the equation of the circle passing through the vertices of the triangle whose sides are along x+y=2, 3x–4y=6 and x–y=0. Find its center and radius. Solution: Let L1 x+y-2=0 L2 3x-4y-6=0 L3  x-y=0 Equation of circle passes through point of intersection of L1, L2 and L3 is

  37. Solution Cont. Equation (i) will represent circle if (a) co-efficient of x2 = co-efficient of y2 (b) co-efficient of xy = 0 from (2):  =-25/7

  38. Solution Cont. Equation of circle is: • (x+y–2)(3x–4y–6)–(1/7)(3x–4y–6)(x–y) • –(25/7)(x–y)(x+y–2)=0  x2+y2–4x+14y–12=0

  39. C(0,6) B(4,0) O(0,0) Class Exercise - 4 Find the equation of a circle which passes through origin, cut positive x and positive y-axis at 4 and 6 units from origin respectively Solution: Diameter,asBOC=900 A (0, 6), B(4, 0)are the end points of diameter. • Equation of circle is: (x–0)(x–4)+(y–0)(y–6)=0 or, x2+y2–4x–6y=0

  40. S2=0 . S1=0 . C2(2,-5) C1(-3,7) Class Exercise - 5 • Find the equation of circle, the end-points of whose diameter are the centers of the circles x2+y2+6x– 14y–1=0andx2+y2–4x+10y–2=0. Solution: Diameter (x+3)(x–2)+(y–7)(y+5)=0 or, x2+y2+x–2y–41=0

  41. Class Exercise - 6 • Find the equation of a circle passes through the points(2,3),(0,–1) and center lies on the line 3x–4y+1=0. Solution: • Let the equation of the circle be • x2+y2+2gx+2fy+c=0 ...(i) -3g+4f+1=0 ...(ii) Centre : (–g,–f) As(2,3) lies on (i)  13+4g+6f+c= 0...(iii) As(0,–1) lies on (i)  1–2f+c=0 ...(iv) Putting g and f in (iii)  c=–3; f=–1; g=–1

  42. Solution Cont. x2+y2+2gx+2fy+c=0…..(i) c=–3; f=–1; g=–1 • Equation of the circle is: • x2+y2–2x–2y–3=0

  43. B(2,2) r=1 A(1,1) Class Exercise - 7 Find the equation of the circle which passes through (1, 1), (2, 2) and radius is 1. Solution: . As it passes through P(1,1) C(h,k)  (h–1)2+(k–1)2=1 h2+k2–2h–2k+1=0 ...(i) As it passes through Q (2,2)  (h–2)2+(k–2)2=1 h2+k2–4h–4k+7=0 ...(ii) (i)—(ii) h+k=3  k=3–h

  44. Solution Cont. h2+k2–2h–2k+1=0 ...(i) h2+k2–4h–4k+7=0 ...(ii) k=3–h From (i): h2+(3–h)2–2h–2(3–h)+1=0 h=1,2  2h2–6h+4=0 h2–3h+2=0 for h=1,k=2; for h=2,k=1 Equation of the circle is (x–1)2+(y–2)2=1 (x–2)2+(y–1)2=1

  45. Class Exercise - 8 If one end of diameter of circle x2+y2–4x–6y+11=0 is (8,4). Find the co-ordinate of other end? Solution: Center of the circle is (2,3) Let the other end be (a,b) other end is (–4, 2)

  46. Class Exercise - 9 Find the equation of circle touching x+y=2 and 2x+2y=3 and passing through (1,1)

  47. x+y=2 2x+2y=3 Solution P(1,1) Observe: 1. x+y=2 and 2x+2y=3 are the parallel lines. Q Diameter of the circle= Distance between the parallel lines. 2. Point (1,1) lies on x+y=2 Line through P and perpendicular to the parallel line is diameter of circle It intersect 2x+2y=3 at diametrically opposite point.

  48. P(1,1) x+y=2 Q 2x+2y=3 Solution Cont. PQ is the diameter of the circle,which is r to the given lines. Slope of the parallel lines =–1 x=y Slope of PQ = 1  y = x 2x+2y=3 x=y Q intersection of

  49. P(1,1) x+y=2 Q 2x+2y=3 Solution Cont. End-Points of the diameter of the circles are P(1,1) and Q(3/4,3/4) Equation of the circle is (x–1)(x–3/4)+(y–1)(y–3/4)=0  (x–1)(4x–3)+(y–1)(4y–3) = 0  4x2–7x+4y2–7y+6=0

  50. Class Exercise - 10 • If the equation of a circle is ax2+(2a–3)y2–4x–1=0 then the centre is • (2,0) (b)(2/3,0) (c) (-2/3,0) (d) None of these Solution: If ax2+(2a–3)y2–4x–1=0 represents circle  a=3 a=2a–3 • Equation of circle is: 3x2+3y2–4x–1=0  x2+y2–(4/3)x–1=0 Center: (2/3,0)

More Related