Graph
1.01k likes | 1.42k Vues
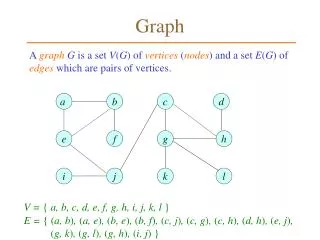
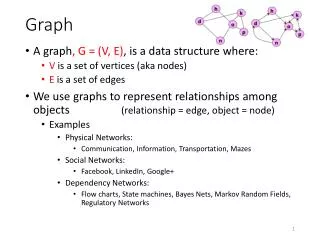
Graph. Definition. G= (V,E) where V is a set of nodes and E is a set of Edges Let |V| be # nodes and let |E| be # Edge in the graph Direct Graph VS Undirect Graph. Directed graph. Undirected graph. Representation. Adjacency matrix For Dense graph

Graph
E N D
Presentation Transcript
Definition • G= (V,E) whereV is a set of nodes and E is a set of Edges • Let|V| be # nodes and let|E|be #Edge in the graph • Direct Graph VS Undirect Graph
Directed graph Undirected graph
Representation • Adjacency matrix • For Dense graph • Use matrix or array of size|V|x|V| โwhere each a[i,j]
Node 0 1 2 3 Adjacency Matrix 4
Node Adjacency Matrix in C int adj_mat[MAXNODES][MAXNODES] = { {0, 1,1,0,1}, {0, 0,1,1,0}, {0, 0,0,0,1}, {0, 1,0,0,1}, {0, 1,0,0,0}};
0 1 3 2 4 Node
Node 0 1 2 3 4
Representation • Adjacency list • For Sparse graph • Use array of Adjacency list of size |V|
1 2 4 2 3 0 4 1 4 1 1 2 Adjacency List 3 4
1 2 4 2 3 4 1 4 1 typedef struct edge_list { int nodeto; struct edge_list *next; } EDGE; typedef struct node { int nodefrom; EDGE *adj; } NODE; Adjacency List in C
nodeto next EDGE nodefrom adj nodefrom adj NODE node_array[0] node_array[1] NODE nodefrom adj
0 1 2 3 4 Finding root of Graph fromAdjacency Matrix Root of Directed Graph is a set of nodes that have no incoming edges. Root ={0} Child Node of0 ...... Parent Node of2 .....
0 1 2 3 4 Finding root of Graph fromAdjacency List
void find_root(NODE node_list[]) { int i,j,r=0; int isroot=0, node; EDGE *ptr; int root_array[MAXNODES]; for ( i=0; i < MAXNODES; i++) { node = node_list[i].nodefrom; isroot = 1; for (j=0; j < MAXNODES && isroot; j++) { ptr = node_list[j].adj; while (ptr != NULL && isroot) { if (ptr->nodeto == node) { isroot = 0; break; } ptr = ptr->next; } } if (isroot) root_array[r++] = node; } printf("roots are "); for (i=0; i < r; i++) printf("%d ",root_array[i]); }
Graph Traversal • Depth First Search • Breadth First Search
Depth First Traversal • Traverse in depth first manner • Use recursive algorithm • Use stack to help remember previous path
Outline of depth-first search Depth_first() { for all u in G u.visit = false; for all u in G if (u.visit == false) traverse(u); } traverse(v) { v.visit = true; for all w adjacent to v if (w.visit = false ) traverse(w); }
start 1 2 0 4 3 8 5 6 7 Time complexity DFS is Depth-first traversal
Breadth First Traversal • Traverse the graph in breadth-first manner • Use queue to store nodes in the same level
Outline of breadth-first search breadh_first() { Queue q; for all u in G u.visit = false; for all u in G if (u.visit == false) { enqueue(q,u); while (not_empty(q)) { w = dequeue(q); if (w.visit ==false) { w.visit = true; for all x adjacent to w enqueue(q,x); } } } }
start enqueue(Q,B), enqueue(Q,E),enqueue(Q,D) Q={B,E,D} 0 A B C Q={A} E D F G H I while (not_empty(q)) { w = dequeue(q); if (w.visit ==false) { w.visit = true; for all x adjacent to w enqueue(q,x); } } Breadth-first traversal
Q={B,E,D} B = dequeue(Q) start enqueue(Q,C) Q={E,D,C} 0 1 A B C E D F G H I while (not_empty(q)) { w = dequeue(q); if (w.visit ==false) { w.visit = true; for all x adjacent to w enqueue(q,x); } } Breadth-first traversal
start 0 1 A B C Q={E,D,C} E= dequeue(Q) Q={D,C} 2 E D F enqueue(Q,G) Q={D,C,G} G H I Breadth-first traversal
start 0 1 A B C Q={D,C,G} D= dequeue(Q) Q={C,G} 2 3 E D F G H I Breadth-first traversal
start Q={C,G} C= dequeue(Q) Q={G} 4 0 1 A B C enqueue(Q,F) Q={G,F} 2 3 E D F G H I Breadth-first traversal
start 4 0 1 A B C 2 3 E D F Q={G,F} G= dequeue(Q) Q={F} enqueue(Q,H) Q={F,H} 5 G H I Breadth-first traversal
start 4 0 1 A B C Q={F,H} F= dequeue(Q) Q={H} 2 6 3 E D F 5 G H I Breadth-first traversal
start 4 0 1 A B C 2 6 3 E D F Q={H} H= dequeue(Q) Q={} 7 5 G H I enqueue(Q,I) Q={I} Breadth-first traversal
start 4 0 1 A B C 2 6 3 E D F 7 8 Q={I} I= dequeue(Q) Q={} 5 G H I Breadth-first traversal
start 0 1 4 2 3 6 8 7 5 Time complexity BFS is Breadth-first traversal
Topological Sort • Order nodes in graph • Mayuse Depth-first or Breadth – first search Time complexity is
Use Breadth-first search. We get order {A,B,C,D} B A C D Topological Sort
start A B C E D F G H I Exercise -What are node orders if breadth-first traversal?
start A B C E D F G H I Exercise - What are node orders if depth-first traversal?
What is the topological order of these nodes? 0 1 2 3 Exercise 4
Weighted Graph • G= (V,E,W) whereV is a set of nodes and E is a set of Edges • W is function mapping from edges to integers representing weight of the corresponding edge
1 1 3 1 2 2 1 1 1 2 Directed graph Undirected graph
Shortest Path in Directed Graphs • Shortest path weight จาก u ไป v คือ andshortest path fromu tov isany path where If there ispath fromu tov otherwise
Shortest Path in Directed Graphs • LetG=(V,E,w) where weight of path as
Shortest Path in Directed Graphs • Single source shortest path finds theshortest path fromsingle source to all nodes in graph • NOTE:w(u,v) may be positive or negative
Dijkstra’s Algorithm • Finding solution forSingle source shortest path problem fornon-negative weight cycle • Negative weight cycle causesno-shortest path fromsource to thedestination
a b -4 When there isnegative weight cycle 3 -1 4 3 6 s c d g 5 8 0 5 11 -3 2 7 e f 3 -6 Froms toc there are many path<s,c>, <s,c,d,c>,<s,c,d,c,d,c>… If cycle <c,d,c> has w=6-3=3 which is positive we still can findshortest path which is 5
a b -4 When there isnegative weight cycle 3 -1 4 3 6 s c d g 5 8 0 5 11 -3 2 7 3 e f - -6 Froms to e, there are paths<s,e>, <s,e,f,e>,<s,e,f,e,f,e>… But cycle <e,f,e> hasw=3-6=-3 which is negative so we get shortest path as -