1 / 8

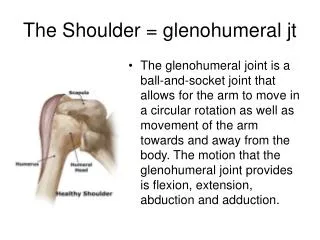
Understanding Inverse and Joint Variation: Models and Applications

This assignment focuses on writing and utilizing inverse and joint variation models. Students will learn to identify and express relationships where one variable varies inversely with another, denoting direct and inverse variations through equations such as y = k/x and z = kxy. The assignment emphasizes practical application by solving example equations and determining the type of variation. Furthermore, it reviews direct variation concepts from Chapter 2, aiding students in mastering the formulation of variation equations for different scenarios.

stephen-gomez
Télécharger la présentation

Understanding Inverse and Joint Variation: Models and Applications

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 9.1 Inverse & Joint Variation

  2. Objectives/Assignment Write and use inverse variation models Write and us joint variation models Assignment: 21-47 odd

  3. Just a reminder from chapter 2 Direct Variation Use y=kx. Means “y varies directly with x.” k is called the constant of variation.

  4. New stuff! Inverse Variation “y varies inversely with x.” k is the constant of variation.

  5. Ex: tell whether x & y show direct variation, inverse variation, or neither. • xy=4.8 • y=x+4 Inverse Variation Hint: Solve the equation for y and take notice of the relationship. Neither Direct Variation

  6. Ex: The variables x & y vary inversely, and y=8 when x=3. • Write an equation that relates x & y. k=24 • Find y when x= -4. y= -6

  7. Joint Variation • When a quantity varies directly as the product of 2 or more other quantities. • For example: if z varies jointly with x & y, then z=kxy. • Ex: if y varies inversely with the square of x, then y=k/x2. • Ex: if z varies directly with y and inversely with x, then z=ky/x.

  8. Examples: Write an equation. • y varies directly with x and inversely with z2. • y varies inversely with x3. • y varies directly with x2 and inversely with z. • z varies jointly with x2 and y. • y varies inversely with x and z.

More Related