1 / 13

Understanding Complex Periodic Data in Oceanography

Learn about deterministic data, equilibrium tides, Fourier series, Cartesian vs. polar notation, Euler's relation, and spectral analysis in the context of oceanographic phenomena. Explore frequency components and harmonic relationships in complex periodic data.

talon
Télécharger la présentation

Understanding Complex Periodic Data in Oceanography

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

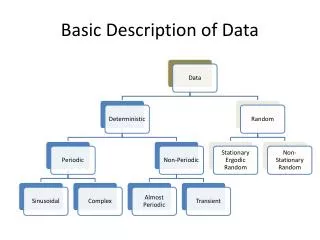
  1. Basic Description of Data

  2. Deterministic Data X o : Initial displacement k: Spring constant m: mass of body t: time k m m 0 m X0 Deterministic Data: They can be explained by an explicit Mathematical relationship Oceanography:Equilibrium Tides can fall in this category

  3. Sinusoidal Periodic Data T, period X : Amplitude fo : Frequency t : Time Θ : Phase +X t -X Discrete or Line Spectra Example: Theoretical M2 Tide X fo f, frequency

  4. Complex Periodic Data • Periodic data that can be described mathematically by varying functions whose waveform exactly repeats itself at regular intervals. Tp= Period (time) the signal repeats itself

  5. Complex Periodic Data (2) • Periodic data can be described using a Fourier Series: Tp = Period (time) the signal repeats itself fo= 1/To, Frequency (fundamental frequency)

  6. Cartesian vs. Polar Notation Vector F has magnitude |F| and angle θ F (a1,b1) Magnitude |F|=sqrt(a12+b12) Angle θ=atan(b1/a1) Y b1 F θ a1 X

  7. From Polar to Complex Notation Vector F has magnitude |F| and angle θ a=|F| cos(θ) b=|F| sin(θ) |F|=sqrt(a2+b2) θ= atan(b/a) Imag j∙b F F=|F| cos(θ)+j∙|F| sin(θ) F=|F|∙(cos(θ)+j∙sin(θ)) θ a b -b Real -θ Euler’s Relation: cos(θ)+j∙sin(θ)=ej∙θ -j∙b F=|F|∙ej∙θ

  8. Vector Multiplication • θ=ω·t+φ, where ω (=2π/T) is the angular frequency and φ initial phase angle at t=0. • θ= (2π/T )·t+φ, and with f=1/T • θ= 2π·f·t+φ • ejθ=ej(2π·f·t+φ)=ej(2π·f·t)∙ejφ • Unit vector that has orientation φ at t=0 and rotates with period T. ej(2π·f·t) ejφ

  9. Complex Periodic Data (3) • An Alternative Presentation of Periodic data is: To= Period fo = 1/To , Frequency i.e., complex periodic data consist of: Static component , Xo Infinite number of sinusoidal components, called harmonics with amplitudes Xnand phases Θn. The frequencies of the harmonic components are all integral multiples of fo

  10. Complex Periodic Data (4) • Assume a signal of consisting of 3 frequency components, f= 60, 75 and 100Hz. • The highest common divider is 5 (so 5Hz is the fundamental frequency fO) so that: • 5Hz ∙ 12 = 60Hz → fO ∙ 12 = 60Hz → n=12 • 5Hz ∙ 15 = 75Hz → fO ∙ 15 = 75Hz → n=15 • 5Hz ∙ 20 =100Hz → fO ∙ 20 = 100Hz → n=20 Discrete or Line Spectra X15 X12 X20 12∙fo 15∙fo 20∙fo f, frequency

  11. Almost Periodic Data 2πn1fo=2π → fo=1/n1 n1/n2=2/3 n1/n3=2/7 n3/n2=sqrt(50)/3 2πn2fo=3π → fo=3/2n2 2πn3f3=7π → fo=7/2n3 n no integers, but rational numbers (sqrt(50) no integer, sqrt(50)/3 no rational) THERE IS NOT A FUNDAMENTAL FREQUENCY, OR IT IS 0 (T=∞)

  12. Transient no Periodic Data

  13. |X(f)| A/a A Fourier transform will give Continuous spectra, no discrete spectra f aA/(a2+b2) In polar notation f cA f

More Related