1 / 21

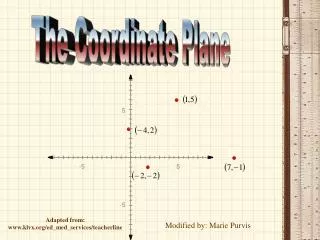
3.5 Lines in the Coordinate Plane

3.5 Lines in the Coordinate Plane. Chapter 3: Parallel and Perpendicular Lines. 3.5 Lines in the Coordinate Plane. Slope-Intercept Form: y = mx + b m: slope b: y -intercept (x, y): point. Slope-Intercept Form. Identify the slope and y -intercept for each:

tavi
Télécharger la présentation

3.5 Lines in the Coordinate Plane

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 3.5 Lines in the Coordinate Plane Chapter 3: Parallel and Perpendicular Lines

  2. 3.5 Lines in the Coordinate Plane Slope-Intercept Form: y = mx + b m: slope b: y-intercept (x, y): point

  3. Slope-Intercept Form Identify the slope and y-intercept for each: a. y = 3x + 2 b. y = -2x + 5 c. y = ½x – 5 d. y = 3x – ½ e. y = -5x – 4 f. y = 0.2x + 0.7

  4. Graphing Lines in Slope-Intercept Form • Graph the line y = 3/4x + 2 m = b = • Graph the line y = x + 2 m = b = • Graph the line y = 3x + 4 m = b =

  5. Graphing Lines in Slope-Intercept Form • Graph the line y = -½x – 2 m = b = • Graph the line y = ½x – 1 m = b = • Graph the line y = -5/3 x + 2 m = b =

  6. Standard Form Ax + By = C (3x + 2y = 5) To Graph from Standard Form, find the x- and y- intercepts: To find the x-intercept, plug in 0 for y. To find the y-intercept, plug in 0 for x.

  7. Graphing Using Intercepts • Graph 6x + 3y = 12 Find the x-intercept: Find the y-intercept:

  8. Graphing Using Intercepts • Graph -2x + 4y = -8 Find the x-intercept: Find the y-intercept:

  9. Transforming to Slope-Intercept Form • Graph 4x – 2y = 9, using slope-intercept form:

  10. Transforming to Slope-Intercept Form • Graph -5x + y = -3, using slope-intercept form:

  11. Write each equation in slope-intercept form and graph the line: • y = 2x + 1 • y – 1 = x • y + 2x =4 • 8x + 4y = 16 • 2x + 6y = 6 • ¾x – ½y = 1/8

  12. Point-Slope Form y – y1 = m(x – x1) (1, 3) and slope 2: (y – 3) = 2(x – 1) y – y1 = m(x – x1)

  13. Using Point-Slope Form • Write an equation of the line through point P(-1, 4) with slope 3. y – y1 = m(x – x1) y – y1 = m(x – x1)

  14. Using Point-Slope Form • Write an equation of the line through point P(2, -4) with slope -1.

  15. Write an equation of the line in point-slope form: • P(2, 3), slope = 2 • I(4, -1), slope = 3 • R(-2, -6), slope = -4 • A(6, 1), slope = ½ • T(-3, 5), slope -1 • E(0, 4), slope 1

  16. Writing an Equation of a Line Given Two Points: • Write an equation of the line through A(-2,3) and B(1,-1): Find the slope: Use one point and write the equation in point-slope form:

  17. Writing an Equation of a Line Given Two Points: • Write an equation of the line through P(5,0) and Q(7,-3) Find the slope: Use one point and write the equation in point-slope form:

  18. Write an equation in point-slope form of the line that contains the given points: • D(0,5) E(5,8) • F(6,2) G(2,4) • H(2,6) I(-1,3) • J(-4,4) K(2,10) • L(-1,0) M(-3,-1) • N(8,10) O(-4,2)

  19. Equations of Horizontal and Vertical Lines: • A Horizontal Line cuts through the y-axis, so the equation is y = • A Vertical Line cuts through the x-axis, so the equation is x = y = 4 x = 3

  20. Equations of Horizontal and Vertical Lines: • Write the Equations of the Horizontal and Vertical line that goes through the point: • (3, 2) Horizontal: Vertical: • (4, 7) Horizontal: Vertical: • (2, 6) Horizontal: Vertical:

  21. Homework • pg 155 1-37all • Workbook 3.5 All Show all work on a separate sheet of paper

More Related