1 / 34

Quadratics

Quadratics. Quadratics. Quadratics. Quadratics. Quadratics. Quadratics. Quadratics.

taylor-dillard
Télécharger la présentation

Quadratics

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Quadratics

  2. Quadratics

  3. Quadratics

  4. Quadratics

  5. Quadratics

  6. Quadratics

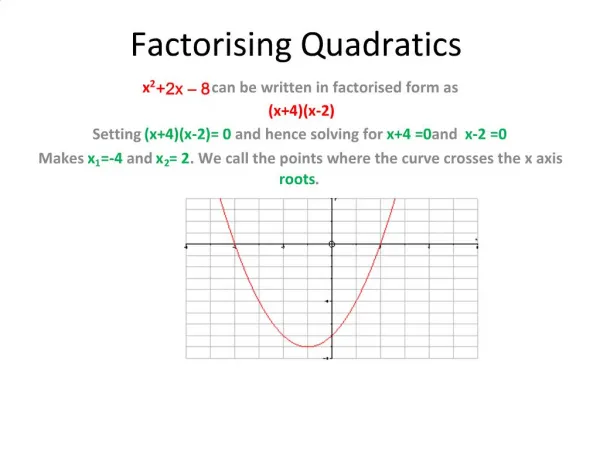
  7. Quadratics • The quadratic equation is used to find the curve on a Cartesian grid. It is primarily used to find the curve that objects take when they fly through the air. For example a softball, tennis ball, football, baseball, soccer ball, basketball, etc.

  8. Quadratics • It also used to design any object that has curves and any specific curved shape needed for a project. The military uses the quadratic equation when they want to predict where artillery shells hit the earth or target when fired from cannons. So if your goal is to go into the military and work with artillery or tanks, you will be using the quadratic equation on a daily basis.

  9. Quadratics • Other uses of the quadratic equation include explaining how planets in our solar system revolve around the sun. Our planets were initially tracked by early scientists, who did not have the advantage of computers, and they used the quadratic equation to determine how planets in our solar system do not have circular orbits - they have elliptical orbits.

  10. Quadratics • We will start slow, we will first review the distributive property, then we will reverse the distributive property. This is called factoring. • Since quadratics are curves we have to know the “roots” of the equation. To do this we will need to understand factoring. • Again we will learn about Quadratics in a slow step by step process.

  11. ObjectivesThe student will be able to: 1. find the prime factorization of a number. 2. find the greatest common factor (GCF) for a set of monomials.

  12. A prime numberis a number that can only be divided by only one and itself. A composite numberis a number greater than one that is not prime. Prime or composite? 37 prime 51 composite

  13. Prime or Composite?89 • Prime • Composite • Both • Neither

  14. Prime or Composite?46 • Prime • Composite • Both • Neither

  15. Prime or Composite?121 • Prime • Composite • Both • Neither

  16. Prime or Composite?1 • Prime • Composite • Both • Neither

  17. Prime or Composite?75 • Prime • Composite • Both • Neither

  18. 1) Find the prime factorization of 84. 84 = 4 • 21 = 2 • 2 • 3 • 7 = 22 • 3 • 7 2) Find the prime factorization of -210. -210 = -1 • 210 = -1 • 30 • 7 = -1 • 6 • 5 • 7 = -1 • 2 • 3 • 5 • 7

  19. 3) Find the prime factorization of 45a2b3 45a2b3 = 9 • 5 • a • a • b • b • b = 3 • 3 • 5 • a • a • b • b • b = 32 • 5 • a • a • b • b • b Write the variables without exponents.

  20. What is the prime factorization of 48? • 3  16 • 3  4  4 • 2  2  3  4 • 2  2  2  2  3

  21. The Greatest Common Factor (GCF)of 2 or more numbers is the largest number that can divide into all of the numbers. 4) Find the GCF of 42 and 60. Write the prime factorization of each number.

  22. 4) Find the GCF of 42 and 60. • = 2 • 3 • 7 • 60 = 2 • 2 • 3 • 5 What prime factors do the numbers have in common? Multiply those numbers. The GCF is 2 • 3 = 6 6 is the largest number that can go into 42 and 60!

  23. 5) Find the GCF of 40a2b and 48ab4. 40a2b = 2 • 2 • 2 • 5 • a • a • b 48ab4 = 2 • 2 • 2 • 2 • 3 • a • b • b • b • b What do they have in common? Multiply the factors together. GCF = 8ab

  24. What is the GCF of 48 and 64? • 2 • 4 • 8 • 16

  25. What is the GCF of 48a2b and 64ab? • 8ab • 16 • 16a2b • 16ab

  26. What is the GCF of 30 and 60? • 2 • 5 • 10 • 15 • 20 • 30

  27. What is the GCF of 48 and 64? • 2 • 4 • 8 • 16

  28. What is the GCF of a2b3c and ab3c2? • abc • a2b2c2 • ab3c • a2b3

  29. Find the GCF of each 42y2, 51x2y2, 15y2 3y2

  30. Find the Product 3x(4x-5) 12x2-15x

  31. Find the Product 7v3(3v4+5) 21v7+35v3

  32. Factor the common factor out of each expression. 6a4+2ab 2a(3a3+b) Can we check our answers?

  33. Factor the common factor out of each expression. 12x3-4x 4x(3x2-1) Why do we need the 1?

  34. Factor the common factor out of each expression. 9u4v2-12u3v3+6uv 3uv(3u3v-4u2v2+2uv)

More Related