1 / 13

ANALYZING GRAPHS OF FUNCTIONS

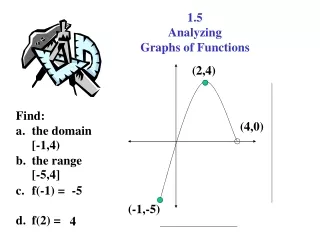
ANALYZING GRAPHS OF FUNCTIONS. We have talked about functions We have talked about graphs Let’s talk about functions AS graphs. Find the Domain and Range. Use graph to evalaute function. Evaluate: f(-3) f(1) f(4) f(2). Zeros of a function.

tayte
Télécharger la présentation

ANALYZING GRAPHS OF FUNCTIONS

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. ANALYZING GRAPHS OF FUNCTIONS

  2. We have talked about functions • We have talked about graphs • Let’s talk about functions AS graphs

  3. Find the Domain and Range

  4. Use graph to evalaute function Evaluate: f(-3) f(1) f(4) f(2)

  5. Zeros of a function • The ZEROS OF A FUNCTION, f, are the x-values for which f(x) = 0 • These are the x-values where the function crosses the x-axis.

  6. To find the zeros • Set the function equal to zero and solve for x • Graph the function and note where it crosses the x-axis

  7. Practice • f(x) = 3x2 + x – 10 • h(x) = 2x + 3

  8. Change in Functions • INCREASING: A function f is increasing on an interval if, for any a, b in the interval, a < b  f(a) < f(b) • DECREASING: A function f is decreasing on an interval if, for any a, b in the interval, a < b  f(a) > f(b) • CONSTANT: A function f is constant on an interval if, for any a, b in the interval, a < b  f(a) = f(b)

  9. Where are these functions increasing? Decreasing? Constant?

  10. Draw a function that: • Increases from (-∞, -11) • Decreases from (-11, -2.5) • Increases from (-2.5, 8) • Is constant from (8, ∞)

  11. Relative Minimum, Maximum • RELATIVE MINIMUM: f(a) is a relative minimum of f if there exists an interval (x, y) that contains a such that for any b, x<b<y  f(a)<f(b) • Rewrite in a way that is easier to read!

  12. Relative Minimum and Maximum • RELATIVE MAXIMUM: f(a) is a relative minimum of f if there exists an interval (x, y) that contains a such that for any b, x<b<y  f(a)>f(b)

  13. Relate the new topics to things we studied a few days ago…Match up and explain how they are related. • Domain and range • Evaluate using algebra • Zeros of a function • Increasing/Decreasing/Constant functions • Evaluate function using a graph • X-intercepts • Slope • Input and output

More Related