1 / 31

De-Noising Signals: A Wavelet Approach

De-Noising Signals: A Wavelet Approach. S. Ezekiel, W. Oblitey, R Trimble Computer Science Department Indiana University of Pennsylvania Indiana, PA 15705. Introduction. Past 3 decades– DSP fast growing fields Signal is a function of independent variable ( time, distance, position..)

vaughan
Télécharger la présentation

De-Noising Signals: A Wavelet Approach

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. De-Noising Signals: A Wavelet Approach S. Ezekiel, W. Oblitey, R Trimble Computer Science Department Indiana University of Pennsylvania Indiana, PA 15705

  2. Introduction • Past 3 decades– DSP fast growing fields • Signal is a function of independent variable ( time, distance, position..) • Analog signal- operation done on time domain • Digital signal- both domain( time and frequency) • Multi-band spectral subtraction– Wu, Hidden Markov model– Sameti et al. --- Noise Masking algorithm – Virag---- Weighted Linear • These Models--Variable degree of success- depending on the goals and assumptions • Our goal:-develop a model to reduce various noises and improve the quality of a signal

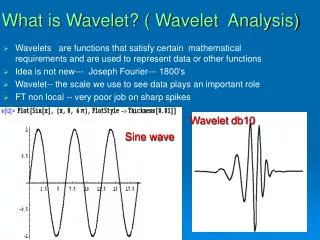
  3. What is Wavelet? ( Wavelet Analysis) • Wavelets are functions that satisfy certain mathematical requirements and are used to represent data or other functions • Idea is not new--- Joseph Fourier--- 1800's • Wavelet-- the scale we use to see data plays an important role • FT non local -- very poor job on sharp spikes Waveletdb10 Sine wave

  4. History of wavelets • 1807 Joseph Fourier- theory of frequency analysis-- any 2pi functions f(x) is the sum of its Fourier Series • 1909 Alfred Haar-- PhD thesis-- defined Haar basis function---- it is compact support( vanish outside finite interval) • 1930 Paul Levy-Physicist investigated Brownian motion ( random signal) and concluded Haar basis is better than FT • 1930's Littlewood Paley, Stein ==> calculated the energy of the function 1960 Guido Weiss, Ronald Coifman-- studied simplest element of functions space called atom • 1980 Alex Grossmann (physicist) Jean Morlet( Engineer)-- broadly defined wavelet in terms of quantum mechanics • 1985 Stephane Mallat--defined wavelet for his DSP ( Ph.D. thesis) • Y. Meyer constructed first non trivial wavelet. • 1988 Ingrid Daubechies-- used Mallat work constructed set of wavelets • The name emerged from the literature of geophysics, by a route through France. The word onde led to ondelette. Translation wave led to wavelet-- by Jean Morlet

  5. Fourier Series and Energy

  6. Fourier, Haar • Amplitude, time  amplitude , frequency • 1965 Cooley and Tukey – Fast Fourier Transform • Haar

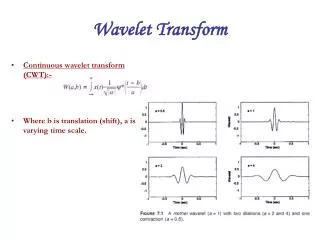
  7. Wavelets Fourier Transform CWT = C( scale, position)= Scaling wave means simply Stretching (or Shrinking) it Shifting f (t) f(t-k)

  8. Wavelet Decomposition and Reconstruction • Calculating coefficients for C at every scale– lots of work • Choose a subset– powers of 2’s dyadic scales ==> DWT • Efficient way of calculating coefficients– by using filters– defined by Mallat-- => FWT( 2 channel sub-band coder)=>decompose signal into 2 parts: approximate (low= actual content) and detail (high=flavor) • The above is called decomposition of Level 1 • This process can be iterated => signal broken down into many low-resolutions. • The procedure to reconstruct the original signal from its decomposed parts is called Reconstruction

  9. Transforms • Transform of a signal is a new representation of that signal • Example:- signal x0,x1,x2,x3 define y0,y1,y2,y3 • Questions • 1. What is the purpose of y's • 2. Can we get back x's • Answer for 2: The Transform is invertible-- perfect reconstruction • Divide Transform in to 3 groups • 1. Lossless( Orthogonal)-- Transformed Signal has the same length • 2. Invertible (bi-orthogonal)-- length and angle may change-- no information lost • 3. Lossy ( Not invertible)--

  10. Answer to Q1: Purpose • IT SEES LARGE vs SMALL • X0=1.2, X1= 1.0, x2=-1.0, x3=-1.2 • Y=[2.2 0 -2.2 0] • Key idea for wavelets is the concept of " SCALE" • We can take sum and difference again==> recursion => Multiresolution • Main idea of Wavelet analysis– analyze a function at different scales– mother wavelet use to construct wavelet in different scale and translate each relative to the function being analyzed • Z=[ 0 0 4.4 0 ] • Reconstruct =====>compression 4:1

  11. Scaling function and Wavelets • corresponding to low pass--> there is scaling function • corresponding to high pass--> there is wavelet function • dilation equation--> scaling function • In terms of original low pass filters • we have • for h(0) and h(1) = 1/2 we have • the graph compressed by 2 gives and shifted by 1/2 gives • By similar way the wavelet equation

  12. Multiresolution Analysis

  13. Signals and Signal Applications • There are various types of signals: • Heart Rate Variability (HRV) • Seismic Signals • Speech Signals • Noise is mixed during the data collection phase • x(t) = a(t) + d(t)

  14. ECG Signal with Noise

  15. Thresholding • Transformation of an input signal to an output signal where is the Threshold value

  16. Signal Enhancement Model • Several traditional methods, such as median filtering, averaging with various masks, and histogram have been studied and implemented • Each of these methods are designed to filter a specific type of noise, for example white, Gaussian, impulsive, additive, quantization, or multiplicative noise.

  17. Step 1: Data Collection. A total of 57 signals were collected for study. We collected 11 speech, 14 HRV, 30 Seismic, and 2 Historic Stock Market signals. • Step 2: Resample. We added noises to test our model against. • River • car engine • air conditioner • highway traffic

  18. Step 3: Wavelet Decomposition. Choose a wavelet. Decide the number of levels then, compute wavelet decomposition for levels. This process separates the signal into two parts, low frequency (approximate coefficients ) and high frequency (detailed coefficients). • Step 4: Remove Noises by Thresholding • Choose the threshold value and type. • Apply the thresholding technique to only the high frequency part of level • This clears out most background noise • Step 5: Reconstruction. Perform wavelet reconstruction from the approximate coefficients in step 4.

  19. Error Measures • We used the two commonly used measure to test the quality of our signal • Root Mean Square (RMS) error • The Peak Signal-to-Noise Ratio

  20. Speech Signal (male subject)

  21. Heart Rate Variability (male, age 48, 8% heart disease, 24 hour sample)

  22. Seismic Signal (24 hour sample)

  23. Dow Jones (5 day sample from 1888-1990)

  24. Speech Signal (female)

  25. We calculated the PSNR for the de-noised signals and we obtained the values 56.1370, 38.6432, 62.5, 32.568, and 27.1034 respectively. This clearly shows that our model efficiently removed the various noises. Further our model retained 98.8015%, 99.9623%, 99%, 99.47%, and 88.4015% of the original content of the signal even after removing 26.8812%, 79.5370%, 82%, 82.1181%, and 80.95% of the detail coefficients, respectively.

  26. Conclusion • A framework using wavelet and multiresolution analysis based noise removal was presented. • This approach offers high quality and flexibility since: • Parameters can be easily modified to remove various noises • Threshold values can be automatically calculated and adjusted based on the waveform. • Although these techniques have been shown to de-noise signals, further experimental analysis is needs fine-tune the various parameters.

  27. JPEG (Joint Photographic Experts Group) • 1. Color images ( RGB) change into luminance, chrominance, color space • 2. color images are down sampled by creating low resolution pixels – not luminance part– horizontally and vertically, ( 2:1 or 2:1, 1:1)– 1/3 +(2/3)*(1/4)= ½ size of original size • 3. group 8x8 pixels called data sets– if not multiple of 8– bottom row and right col are duplicated • 4. apply DCT for each data set– 64 coefficients • 5. each of 64 frequency components in a data unit is divided by a separate number called quantization coefficients (QC) and then rounded into integer • 6. QC encode using RLE, Huffman encoding, Arithmetic Encoding ( QM coder) • 7. Add Headers, parameters, and output the result • interchangeable format= compressed data + all tables need for decoder • abbreviated format= compressed data+ not tables ( few tables) • abbreviated format =just tables + no compressed data • DECODER DO THE REVERSE OF THE ABOVE STEPS

  28. JPEG 2000 or JPEG Y2k • divide into 3 colors • each color is partitioned into rectangular, non-overlapping regions called tiles– that are compressed individually • A tile is compressed into 4 main steps • 1. compute wavelet transform – sub band of wavelets– integer, fp,---L+1 levels, L is the parameter determined by the encoder • 2. wavelet coeff are quantized, -- depends on bit rate • 3. use arithmetic encoder for wavelet coefficients • 4. construct bit stream– do certain region, no order • Bit streams are organized into layers, each layer contains higher resolution image information • thus decoding layer by layer is a natural way to achieve progressive image transformation and decompression

  29. Wavelet Packet • Walsh-Hadamard transform-- complete binary tree --> wavelet packet • "Hadamard matrix"==> all entries are 1 and -1 and all rows are orthogonal-- divide two time by sqrt(2)==> orthogonal & symmetric • Compare with wavelet-- computations sums z0=0 sums y0 and y2 difference z2=4.4 x sums z1=0.4 difference y1 and y3 difference z3=0

  30. Filters and Filter Banks • Filter is a linear time-invariant operator • It acts on input vector x --- Out put vector y is the convolution of x with a fixed vector h • h--> contains filter coefficients-- our filters are digital not analog-- h(n) are discrete time t= nT, • T is sampling period assume it is 1 here • x(n) and y(n) comes all the time t= 0, +_ 1.... • y(n) = Σh(k) x(n-k) = convolution h* x in the time domain • Filter Bank= Set of all filters • Convolution by hand--- arrange it as ordinary multiplication -- but don't carry digits from one column to another • x= 3 2 4 h= 1 5 2 • x * h = 3 17 20 24 8

More Related