1 / 8

Mixing Paint

This guide explains how to use rational equations to solve paint mixing problems involving yellow and blue paint. Learn to create specific shades of green by mixing different proportions of yellow paint. The tutorial includes examples such as achieving an 80% yellow mixture, as well as exploring alternative mixtures like 75% and 20% yellow. Additionally, the concepts apply to calculating batting averages and basketball free throw percentages using similar rational equations. Understand the methodology through cross-products and find the preferred methods for solving mixture equations.

vega
Télécharger la présentation

Mixing Paint

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Mixing Paint Rational Equations

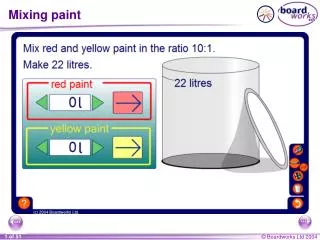
  2. Paint Mixing 1) You have a 12 pint mixture of paint that is made up of equal amounts of blue paint and yellow paint. You need to create a special shade of green for your art class project. The special shade of green is 80% yellow. How many pints of yellow paint do you need to add to the mixture? Solve this problem by using a rational equation. Start with a verbal model. Now use Cross-Products to solve.

  3. Use a Rational Equation. • What if you needed a paint mixture that is 75% yellow? How many pints of yellow paint would you need to add to the mixture? • What if you needed a paint mixture that was 20% yellow? How many pints of yellow paint would you need to add? What is the problem with this answer? What is another way to approach this problem and create a mixture that is 20% yellow by still using a rational equation?

  4. Other methods to solve the paint mixture problem. Use a different method to solve the following mixture problem. • You have a mixture of paint that is made up of 4 pints of yellow and 8 pints of blue paint. How many pints of yellow need to be added to get a 75% yellow mixture? • What if we wanted a 50% mixture? Now that you have tried different methods, which do you prefer and why?

  5. Use rational equations to solve the following problems. • Batting average is calculated by dividing the number of hits by the number of times at bat. A player has been at bat 90 times and has a batting average of .200. How many consecutive hits would the player need to raise the average to .250? • A basketball player has made 40% of 30 free throw attempts so far. How many consecutive free throws must he make to raise his percent to 50? To 60?

  6. Extension Write a problem that can be solved by using a rational equation. Use cross products to solve it.

  7. Solutions Ans: y= 18 pints Ans: y= 12 pints Ans: y= - 4.5 pints (this works mathematically but not in the real world) So we should solve for blue Ans: b= 18 pints Ans: 20 pints of yellow Ans: 4 pints of yellow

  8. Solutions (continued) • Let x = original number of hits • substitutex = 18 into proportion • Let h = number of • Additional hits • Ans: h = 6 more hits • Ans: 6 consecutive free throws for 50% and 15 consecutive free throws for 60%.

More Related