1 / 40

Exploring Radiosity and Interreflections in Rendering: Lecture Insights

Discover how radiosity and interreflections impact the realism of 3D scenes through a detailed lecture on the rendering process. Learn about the importance of indirect lighting, realism factors, and solving the rendering equation. Delve into the concepts of irradiance, form factors, and matrix inversion techniques for radiosity computations. Gain insights on approaches for wireframe rendering, classical methods, and a two-pass solution integrating radiosity and ray-tracing. Uncover the complexities and solutions of the inverse problem in rendering.

vincent-moody
Télécharger la présentation

Exploring Radiosity and Interreflections in Rendering: Lecture Insights

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Interreflections and Radiosity : The Forward Problem Lecture #11 Thanks to Kavita Bala, Pat Hanrahan, Doug James, Ledah Casburn

  2. Cornell Box blue hue red hue

  3. Phong Shading Plastic looking scene • no object interactions • no shadows

  4. Ray Tracing Scene doesn’t look realistic enough. • where is the corner of room? • is window flush with wall? • is the carpet and wood supposed to be this dark?

  5. Radiosity – today’s topic Indirect lighting affects realism. • room has a corner • window has depth • carpet and wood on table • is lighter • walls look more pink

  6. The Rendering Equation – Graph Style p’’ source viewer p’ p Reflectance from Surfaces Emission (light source) Visibility (shadows)

  7. Diffuse Interreflections - Radiosity • Consider lambertian surfaces and sources. • Radiance independent of viewing direction. • Consider total power leaving per unit area of a surface. • Can simulate soft shadows and color bleeding • from diffuse surfaces. • Used abundantly in heat transfer literature

  8. Irradiance, Radiosity • Irradiance E is the power received per unit surface area • Units: W/m2 • Radiosity • Power per unit area leaving the surface (like irradiance)

  9. Planar piecewise constancy assumption • Subdivide scene into • small “uniform” polygons

  10. Power Equation • Power from each polygon: • Linear System of Equations:

  11. Form Factors Invariant

  12. Form Factor Computation • Schroeder and Hanrahan derived an analytic expression • for polygonal surfaces. • In general, computing double integral is hard. • Use Monte Carlo Integration.

  13. Form Factor Computation

  14. Form Factor Computation

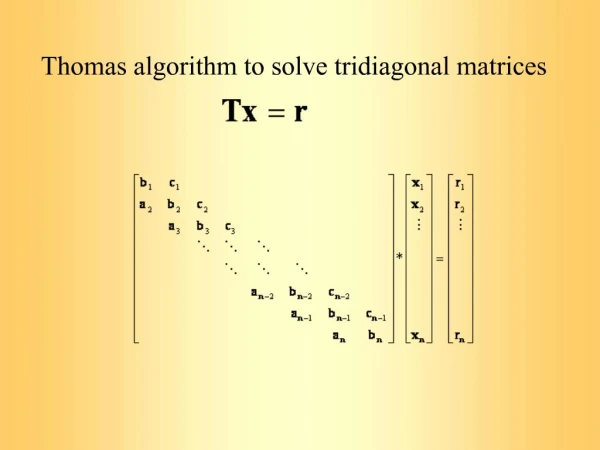
  15. Linear System of Radiosity Equations Known Known Unknown • Matrix Inversion to Solve for Radiosities.

  16. Doug James

  17. Wireframe

  18. Classical • Approach • No • Interpolation

  19. Wireframe

  20. Classical • Approach • Low Res

  21. Classical • Approach • High Res • More accurate

  22. Classical • Approach • High Res • Interpolated

  23. Sample Scenes

  24. Sample Scenes

  25. Sample Scenes

  26. Sample Scenes

  27. Sample Scenes

  28. Summary

  29. Doug James

  30. Two Pass Solution • First Pass: Diffuse Interreflections • View independent, global diffuse illumination • computed with radiosity. • Second Pass: Specular Interreflections • View dependent, global specular illumination • computed with ray-tracing. • Combine strengths of radiosity and ray-tracing.

  31. Interreflections : The Inverse Problem Lecture #12

More Related