1 / 17

Discrete Exterior Calculus

Discrete Exterior Calculus. More Complete Introduction. See Chapter 7 “Discrete Differential Forms for Computational Modeling” in the SIGGRAPH 2006 Discrete Differential Geometry Course Notes Notes are available from http://ddg.cs.columbia.edu , or Google “discrete differential geometry”

wesley-rasmussen
Télécharger la présentation

Discrete Exterior Calculus

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Discrete Exterior Calculus

  2. More Complete Introduction • See Chapter 7 “Discrete Differential Forms for Computational Modeling” in the SIGGRAPH 2006 Discrete Differential Geometry Course Notes • Notes are available from http://ddg.cs.columbia.edu, or Google “discrete differential geometry” • Topology, interpolation, more differential operators.

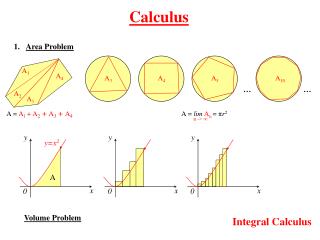
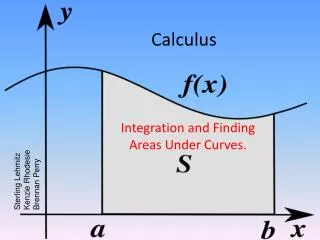
  3. Motivation • We often work on problems where physical or geometric quantities are defined throughout space, on a surface, or on a curve. • When we discretize the geometry, where do we put those quantities? What do the numbers mean? How do we integrate and differentiate them? • DEC provides a scheme that preserves important properties and structures from continuous calculus.

  4. Nutshell: Integration • We discretize geometry as a simplicial complex (triangle mesh, tet mesh) with oriented faces, edges, and vertices. • Where we store quantities corresponds to how we integrate them, i.e. we integrate divergence over volumes so it goes on tets. • Quanities are “pre-integrated.” The stored divergence value on a tet is actually an integral of divergence over the tet. • Integration over a domain is an oriented sum of the numbers on the simplices composing the domain.

  5. Nutshell: Differentiation • The discrete exterior derivative d maps the oriented sum of values on the boundary of a simplex to the simplex. • Think first fundamental theorem of calculus, Gauss’ theorem, Stokes’ theorem. • d is implemented as a matrix of 0, 1, and -1 representing the incidence of k and k+1 simplices. • For instance, it might be a matrix with |E| columns and |F| rows applied to a column vector of |E| values

  6. Nutshell: Dual • Sometimes we have a quantity defined on simplices of one dimension that we would like to integrate on simplices of a different dimension. • The Hodge star transfers a value from a k-simplex to a dual n-k simplex, i.e. from an edge to a dual face in 3D. • The value is transformed based on the difference between the primal and dual geometry. • In the notes, the transformation is a scaling based on the ratio of primal and dual element sizes. • This can be implemented as a diagonal matrix.

  7. Nutshell: Recap • Integration is a weighted sum, think dot product. • Differentiation goes from boundaries to simplices, think incidence matrix. • Hodge star goes from primal to dual elements with a scaling factor, think diagonal matrix.

  8. Simplifcial Complexes

  9. Dual Complex

  10. Boundary Operator

  11. What is a form? • A form is something ready to be integrated, f(x)dx is a form. • (Intuitively) A form is an association of a number with an oriented piece of geometry. • The dimensionality of the differential or domain of integration determines the dimensionality of the form. • 1-forms for curves, 2-forms for surfaces, etc. • Discretely, 1-form is values stored on edges, etc.

  12. Examples

  13. d • Flux lives on faces while divergence lives on tets. • The sum of the flux over the boundary of a volume equals the integral of the divergence over the volume. • Divergence is the discrete exterior derivative of flux. • d takes the sum of values defined on the boundary of a simplex and puts it on the simplex • d is an incidence matrix, the transpose of the boundary operator

  14. d Does Everything • There is one d for each dimensionality of form. • d for 0-forms is gradient, d for 1-forms is curl, d for 2-forms is divergence

  15. Structure Preservation

  16. Hodge Star in Action • A typical 1-form might be based on the dot product of a vector field with the tangent to a curve. • A typical 2-form might be based on the dot product of a vector field with the normal to a surface. • The tangent to an edge is normal to a dual face. • The Hodge star extracts the dot product from the integral over the primal edge and reintegrates it over the dual face.

  17. Circulation and Vorticity • The flux on a face is the integral over the face of a dot product of a velocity vector with the normal to the face. • The circulation on an edge is the integral over the edge of the dot product of the velocity vector with the tangent to the edge. • The Hodge star of flux is circulation. • In the paper, take the discrete derivative of circulation to get vorticity, which is a 2-form.

More Related