Graphs
460 likes | 596 Vues
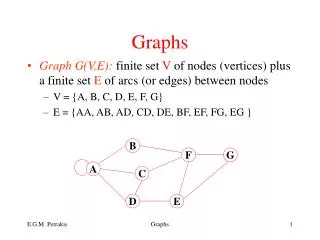
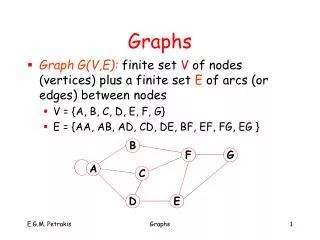
B. F. G. A. C. D. E. Graphs. Graph G(V,E): finite set V of nodes (vertices) plus a finite set E of arcs (or edges) between nodes V = {A, B, C, D, E, F, G} E = {AA, AB, AD, CD, DE, BF, EF, FG, EG }. Terminology. Two vertices are adjacent if they are connected with an edge

Graphs
E N D
Presentation Transcript
B F G A C D E Graphs • Graph G(V,E): finite set V of nodes (vertices) plus a finite set E of arcs (or edges) between nodes • V = {A, B, C, D, E, F, G} • E = {AA, AB, AD, CD, DE, BF, EF, FG, EG } Graphs
Terminology • Two vertices are adjacent if they are connected with an edge • Neighbor vertices • Subgraph of G=(V,E): a graph G’=(V’,E’) where V’, E’ are subsets of V, E • |V| , |E|: number of nodes and edges of G • Complete graph: contains all possible edges • |E| in Θ(|V|2) Graphs
B C A G E D H F • Undirected graphs: the edges are not directed • from one vertex to another Graphs
B C A G E D H F Directed Graphs: the edges are directed Graphs
A A B C B C D D E F G Graphs
Vertex degree : maximum number of incoming or outgoing edges. • In-degree: number of incoming edges • Out-degree: number outgoing edges • RelationRonA: R = {<x,y>| x,y ∊ N} • x < y • x mod y = odd • Labeled graph: labels are associated to vertices or edges • Weighted graph: weights on edges Graphs
1 3 Relation 10 3 Weighted 10 7 3 1 5 8 5 8 17 17 1 5 6 6 Graphs
Vertices (V1,V2,…Vn) form a path if there exist edges from Vi to Vi+1 for 1<= i <= n • V1,V2,…Vn :adjacent • Length of path : number of edges • Weighted graphs: sum of weights on path • Cycle: path (of length 3 or more) connecting a vertex with itself • Cyclic graph : contains cycle • Acyclic graph : does not contain cycle • DAG:Directed Acyclic Graph Graphs
7 0 2 6 4 5 3 1 • An undirected graph is connected if there is at least one path between any two vertices • Connected components: maximally connected subgraphs • Free tree of graph: connected, undirected, acyclic subgraph of the graph • A free tree has |V| nodes and |V|-1 edges Graphs
a a b b a a b b x x a b a b a b c Operations on graphs • join (a,b) • join (a,b,x) • remv[wt] (a,b,x) • adjacent (a,b) adjacent (a,b) = true adjacent (a,c) = false Graphs
Build Graphs read(n); // number of nodes read and create n nodes label them from 1 .. n While not eof(..) { read(node1, node2, w12); joinwt(node1, node2, w12); } any graph algorithm Graphs
0 1 2 3 4 Directed Graph 0 2 0 1 1 1 1 4 2 1 1 3 3 1 4 1 adjacency matrix 0 1 4 1 3 2 4 3 2 adjacency list 4 1 Representation of Directed Graphs Graphs
0 1 2 3 4 Undirected Graph 0 1 1 0 2 1 1 1 1 2 1 1 4 3 1 1 1 4 1 1 1 3 Adjacency Matrix 0 1 4 1 0 3 4 2 3 4 3 1 2 Adjacency List 4 0 1 2 Representation of Undirected Graphs Graphs
Graph Implementation • Matrix representation, Adjacency list • simple implementation • difficult to process edges • unused space in matrix • auxiliary functions and structures • Mark: 1D array marking vertices • Mark[i] = 1 if vertex i has been processed (visited) • typedef int *Edge; • matrix: the actual Graph implemented as an 1D array of size n2 • edge (i, j) is found at matrix[i*n + j] • if edge exists matrix[i*n + j] = wt • otherwise matrix[i*n + j] = NOEDGE Graphs
Class Graph { //Graph class: Adjacency matrix private: int* matrix; //The edge matrix int numVertex; //Number of vertices int numEdge; //Number of edges bool* Mark; //The mark array public: Graph( ); //Constructor ~Graph( ); //Destructor int n( ); //Number of vertices for graph int e( ); //Number of edges for graph Edge first(int); //Get the first edge for a vertex bool isEdge(Edge); //TRUE if this is an edge Edge next(Edge); //Get next edge for a vertex int v1(Edge); //Return vertex edge comes from int v2(Edge); //Return vertex edge goes to int weight(int, int); //Return weight of edge int weight(Edge); //Return weight of edge } Graphs
Graph::Graph( ) { //Constructor Mark = NULL; matrix = NULL;//plus code for creating graph } Graph::~Graph( ) { //Destructor: return allocated space if (Mark != NULL) delete [ ] Mark; if (matrix != NULL) delete [ ] matrix; } int Graph::n( ){ return numVertex; } //Num. of vertices for the graph int Graph::e( ) //Number of edges { return numEdge; } Edge Graph::first(int v) { //Get the first edge for a vertex int stop = (v+1) * numVertex; //Position at end of v’s row for ( int pos = v * numVertex; pos < stop; pos++) //scans entire row if ( matrix[pos] != NOEDGE) return &matrix[pos]; return NULL; } Graphs
bool Graph::isEdge(Edge w) //TRUE if (w,0) is an edge { return w != NULL; } Edge Graph::next(Edge w) { //Get next edge of (w,0) int stop = (v1(w) + 1) * numVertex; //Position at end of row for (int pos = (w – matrix) + 1; pos < stop; pos++) if (matrix[pos] != NOEDGE) return &matrix[pos]; return NULL; } int Graph::v1(Edge w) //Return 1st vertex of edge { return ( w – matrix ) / numVertex; } //Pointer arithmetic int Graph::v2(Edge w) //Return 2nd vertex edge { return ( w – matrix ) % numVertex; } //Pointer arithmetic int Graph::weight( int i, int j) { //Return weight of edge if ( matrix[ i * numVertex + j ] = = NOEDGE ) return INFINITY; else return matrix[ i * numVertex + j ]; } int Graph::weight(Edge w) { //Return weight of edge if ( *w = = NOEDGE ) return INFINITY; else return *w; } Graphs
Class Graph { //Graph class: Adjacency list private: Edge *list; //The vertex list int numVertex; //Number of vertices int numEdge; //Number of edges bool *Mark; //The mark array public: Graph( ); //Constructor ~Graph( ); //Destructor int n( ); //Number of vertices for graph int e( ); //Number of edges for graph Edge first(int); //Get the first edge for a Vertex bool isEdge(Edge); //TRUE if this is an edge Edge next(Edge); //Get next edge for a vertex int v1(Edge); //Return vertex edge comes from int v2(Edge); //Return vertex edge goes to int weight(int, int); //Return weight of edge int weight(weight); //Return weight of edge }; Graphs
class EdgeLink { //A singly-linked list node public: int weight; //Edge weight int v1; //1st vertex of edge int v2; //2nd vertex of edge EdgeLink *next; //Pointer to next edge in list EdgeLink(int vt1, int vt2, int w, EdgeLink *nxt = NULL) //Constructor { v1 = vt; v2 = vt2; weight = w; next = nxt; } }; Typedef EdgeLink* Edge; Graphs
Graph::Graph( ) { //Constructor Mark = NULL; list = NULL; // the code for creating a graph follows } Graph::~Graph( ) { //Destructor: return allocated space if (Mark != NULL) delete [ ] Mark; if (list != NULL) { //Remove all of the edges for (int v = 0; v < n( ); v++) //For each vertex while (list[v] != NULL) { //return its edges Edge temp = list[v]; list[v]= list[v]next; delete temp; } delete [ ] list; //Now remove the vertex list headers } } int Graph::n( ) { return numVertex; } //Number of vertices int Graph::e( ) { return numEdge; } //Number of edges Graphs
Edge Graph::first(int v) //Get the first edge for a vertex {return list[v]; } bool Graph::isEdge(Edge w) //TRUE if this is an edge { return w != NULL; } Edge Graph::next(Edge w) { //Get next edge for a vertex if (w == NULL) return NULL; else return wnext; } int Graph::v1(Edge w) //Return vertex edge comes from { return wv1; } int Graph::v2(Edge w) //Return vertex edge goes to { return wv2; } Graphs
int Graph::weight( int i, int j) { //Return weight of edge for (Edge curr = list[i]; curr != NULL; curr = curr⇢next) if (currv2 = = j ) return curr weight; return INFINITY; } int Graph::weight(Edge w) { //Return weight of edge if ( w = = NULL ) return INFINITY; else return w weight; } Graphs
arcptr info nextnode B A D C E An even better representation ndptr nextarc info: data arcptr: pointer to an adjacent node nextnode: pointer to a graph node ndptr: pointer to adjacent node nextarc: pointer to next edge Graphs
graph C D n i l E n i l n i l n i l Β A <D,B> n i l <C,E> n i l <A,B> <A,C> <A,D> <A,E> Graphs
Graph Traversals • Trees • preorder • inorder • postorder • Graphs • Depth first search • Breadth first search Graphs
Depth First Search: • Starting from vertex v, initially all vertices unvisited void DFS(v) { Mark(v) = true; for each vertex w adjacent to v if (!Mark(w)) DFS(w) } • Complexity DFS : • O(|V| + |E|): adjacency list representation • O(|V|2) in dense graphs • O(|V|2):matrix representation Graphs
v = v1 7 v3 v2 v1 v6 v5 v4 v8 v7 1 1 7 5 6 8 2 2 5 3 3 4 2 4 6 8 8 8 3 DFS :V1V2V4V8V5V6V3V7 v1 v2 v3 v7 v4 v5 v6 v8 Graphs
v = v1 ΒFS : V1V2V3V4V5V6V7V8 v1 v2 v3 v7 v4 v5 v6 v8 Breadth-First Search Graphs
Breadth First Search (BFS): • Starting from vertex |V|, Initially all nodes are“unvisited” • Visit adjacent nodes of current nodes (use a queue) void DFS(v) { visited(v) = true; enqueue(v, Q); while ( Q ≠ 0 ) { x = dequeue(Q); for each y adjacent x do if ! Mark(y) { Mark(y) = TRUE; enqueue(y,Q); } } } Graphs
front rear v4 v2 v3 v3 v1 v5 v8 v4 v7 v8 v7 v5 v6 v5 v8 v6 v7 v6 v6 output(v1) v1 front v2 v3 output(v2) rear v7 v4 v5 v6 output(v3) front front v8 front output(v4) rear rear rear front output(v5) output(v6) front output(v7) v = v1 Graphs
Complexity of BFS: • O(|V|+|E|) : adjacency list representation • d1 + d2 + ...+ dn = |E| • di= degree (vi) • O(|V|2) : adjacency matrix representation Graphs
void DFS (Graph& G, int v){//Depth-First Search action(G,v); G.Mark[v] = VISITED; for ( Edge w = G.first(v); G.isEdge(w); w = G.next(w)) if (G.Mark[G.v2(w)] = = UNVISITED)DFS ( G, G.v2(w)); action(G,v); } void BFS (Graph& G, int start){//Breadth-First Search Queue Q(G.n( )); Q.enqueue(start); G.Mark[start] = VISITED; While ( !Q.isempty( )) { int v = Q.dequeue( ); action(G,v); for ( Edge w = G.first(v); G.isEdge(w); w = G.next(w)) if (G.Mark[G.v2(w)] = = UNVISITED){ G.Mark[G.v2(w)] = VISITED;Q.enqueue(G.v2(w)); } action(G,v); } Graphs
B C A D E F A E B G C D connected components • connected graphs: undirected graph, there is a path connecting any two nodes • unconnected graphs: not always a path Graphs
If there exist unconnected nodes in a DFS or BFS traversal of G then G is unconnected • Find all connected components: void COMP(G, n) { for i = 1 to n if Mark(i) == UNVISITED then DFS(i) [or BFS(i)]; } • Complexity: O(|V| + |E|) Graphs
(G,E) Spanning Trees • Tree formed from edges and nodes of G • Spanning Trees of G: Graphs
Spanning forest ofG = ( V, E ): set of disjoint spanning trees of G • Ti = ( Vi , Ei ) 1≤ i ≤ k where Vi and Ei are subsets of V and E • DFS producesdepth first spanning trees or forest • BFS breadth first spanning trees / forest • Undirected graphs provide more traversals • produce less but short spanning trees • Directed graphs provide less traversals • produce more and higher spanning trees Graphs
DFS spanning tree A A B B C C D E A DFS A D E B F DFS spanning forest DFS B C C E F D D E G G DFS Graphs
A ΒFS A B F B C E C F D D E H H BFS A A BFS spanning tree ΒFS B C D B C D E F G E F G BFS spanning forest Graphs
1 6 5 1 5 5 2 3 4 6 4 2 3 5 6 6 1 1 1 1 1 1 1 1 1 1 5 5 3 3 3 4 2 3 4 2 3 4 4 4 2 4 2 4 2 3 6 6 6 5 6 Minimum Cost Spanning Tree Prim’s algorithm: Complexity O(|V|2) costT = 1 + 5 + 2 + 4 + 3 Graphs
void Prim(Graph& G, int s) { //Prim’s MST algorithm int D[G.n( )]; //Distance vertex int V[G.n( )]; //Who’s closest for (int i=0; i<G.n( ); i++); D[i] = INFINITY; //Initialize D[s] = 0; for ( i=0; i<G.n( ); i++) { //Process the vertices int v = minVertex(G, D); G.Mark[v] = VISITED; if ( v != s ) AddEdgetoMST(V[v], v); //Add this edge to MST if (D[v] = = INFINITY ) return; //unreachable vertices for ( Edge w = G.first(v); G.isEdge(w); w = G.next(w)) if (D[G.v2(w)] > G.weight(w)) { D[G.v2(w)] = G.weight(w); //Update distance and V[G.v2(w)] = v; // who it came from } } } Graphs
void minVertex(Graph& G, int* D){//Find min cost vertex int v; //Initialize v to any unvisited vertex for (int i = 0; i < G.n( ); i++) //Initialize if (G.Mark[i] = = UNVISITED) { v = i; break; } for ( i=0; i<G.n( ); i++) //Now find smallest value if ((G.Mark[i] = = UNVISITED) && ( D[i] < D[v] )) v = i; return v; } Graphs
Dijkstra’s algorithm: find the shortest path from a given node to every other node in a graph G • No better algorithm for single ending node • Notation: • G = (V,E) : input graph • C[i,j] : distance between nodes i, j • V : starting node • S : set of nodes for which the shortest path from v has been computed • D(W) : length of shortest path from v to w passing through nodes in S Graphs
starting point: v = 1 1 10 100 30 2 5 10 60 50 4 3 20 Graphs
function Dijkstra(G: graph, int v) { S = {1}; for i = 2 to n D[i] = C[i,j]; while (S != V) { choose w from V-S: D[w] = minimum S = S + {w}; for each v in V–S: D[v] = min{D[v], D[w]+[w,v]}*; } } * If D[w]+C[w,v] < D[v] then P[v] = w: keep path in array Graphs
void Dijkstra(Graph& G, int s) { // Compute shortest path distances int D[G.n()]; for (int i=0; i <G.n(); i++) // Initialize D[i] = INFINITY; D[s] = 0; for (i=0; i <G.n(); i++) { // Process the vertices int v = minVertex(G, D); if (D[v] == INFINITY) return; // Remaining vertices unreachable G.setMark(v, VISITED); for (Edge w = G.first(v); G.isEdge(w); w = G.next(w)) if (D[G.v2(w)] > (D[v] + G.weight(w))) D[G.v2(w)] = D[v] + G.weight(w); } } Graphs
int minVertex(Graph& G, int* D) { // Find min cost vertex int v; // Initialize v to any unvisited vertex; for (int i=0; i <G.n(); i++) if (G.getMark(i) == UNVISITED) { v = i; break; } for (i++; i <G.n(); i++) // Now find smallest D value if ((G.getMark(i) == UNVISITED) && (D[i] < D[v])) v = i; return v; } minVertex:scans through the list of vertices searching for the min value O(|V|) time Complexity: O(|V|2 + |E|) = O(|V|2) since O(|E|) is O(|V|2) Graphs