Download
1 / 3
30 likes | 172 Vues
This article provides an in-depth explanation of the Merge Sort algorithm and the recursive calculation of the factorial function in C programming. Merge Sort operates with a time complexity of O(n log n), ensuring efficient sorting of large lists. We delve into the implementation details of sorting a list using Merge Sort, as well as how to compute factorial values recursively using the `factR` function. The tutorial is aimed at helping programmers grasp these foundational concepts in computer science with practical code examples.
E N D
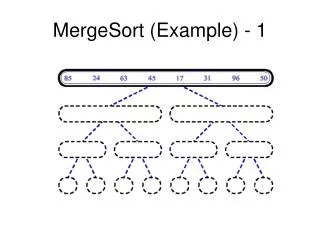
MergeSort • O(n log n), Ω(n log n) Sort (list of n) Ifn<2,return. Else Sort(lefthalf). Sort(righthalf). Mergesortedhalves.
int main (void) { int ans = factR(5); } int fact(5) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } How it happens int fact(4) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } int fact(3) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } int fact(2) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } int fact(1) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } int fact(0) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); }
int main (void) { int ans = factR(5); return 0; } int fact(5) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } How it happens 1 ans = 120! int fact(4) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } 1 int fact(3) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } 2 int fact(2) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } int fact(1) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } 6 ( 24 ) int fact(0) factR (int numR) { //base case! if (numR <=1) return 1; else return numR * factR(numR-1); } ( 6 ) 24 ( 2 ) ( 1 ) 120 ( 1 )
