Statistical Techniques I
280 likes | 425 Vues
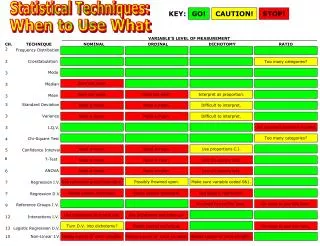
Statistical Techniques I. EXST7005. Simple Linear Regression. Measuring & describing a relationship between two variables Simple Linear Regression allows a measure of the rate of change of one variable relative to another variable.

Statistical Techniques I
E N D
Presentation Transcript
Statistical Techniques I EXST7005 Simple Linear Regression
Measuring & describing a relationship between two variables • Simple Linear Regression allows a measure of the rate of change of one variable relative to another variable. • Variables will always be paired, one termed an independent variable (often referred to as the X variable) and a dependent variable (termed a Y variable). • There is a change in the value of variable Y as the value of variable X changes. Simple Linear Regression
Y X Simple Linear Regression (continued) • For each value of X there is a population of values for the variable Y (normally distributed).
Simple Linear Regression (continued) • The linear model which discribes this relationship is given as • Yi = b0 + b1Xi • this is the equation for a straight line • where; b0 is the value of the intercept (the value of Y when X = 0) • b1 is the amount of change in Y for each unit change in X. (i.e. if X changes by 1 unit, Y changes by b1 units). b1 is also called the slope or REGRESSION COEFFICIENT
Simple Linear Regression (continued) • Population Parameters • my.x = the true population mean of Y at each value of X • b0 = the true value of the Y intercept • b1 = the true value of the slope, the change in Y per unit of X • my.x = b0 + b1Xi • this is the population equation for a straight line
The sample equation for the line describes a perfect line with no variation. In practice there is always variation about the line. We include an additional term to represent this variation. • my.x = b0 + b1Xi + ei for a population • Yi = b0 + b1Xi + ei for a sample • when we put this term in the model, we are describing individual points as their position on the line, plus or minus some deviation Simple Linear Regression (continued)
Y X Simple Linear Regression (continued)
Simple Linear Regression (continued) • the SS of deviations from the line will form the basis of a variance for the regression line • when we leave the ei off the sample model, we are describing a point on the regression line predicted from the sample. To indicate this we put a HAT on the Yi value
Characteristics of a Regression Line • The line will pass through the point `X,`Y (also the point 0, b0) • The sum of squared deviations (measured vertically) of the points from the regression line will be a minimum. • Values on the line can be described by the equation Y = b0 + b1Xi
Y X • Fitting the line starts with a corrected SSDeviation, this is the SSDeviation of the observations from a horizontal line through the mean. Fitting the line
Y X • The fitted line is pivoted on the point until it has a minimum SSDeviations. Fitting the line (continued)
How do we know the SSDeviations are a minimum? Actually, we solve the equation for ei, and use calculus to determine the solution that has a minimum of Sei2. Fitting the line (continued)
The line has some desirable properties • E(b0) = b0 • E(b1) = b1 • E(`YX) = mX.Y • Therefore, the parameter estimates and predicted values are unbiased estimates. Fitting the line (continued)
Y = the "dependent" variable, the variable to be predicted • X = the "independent" variable, also called the regressor or predictor variable. • Assumptions - general assumptions • Y variable is normally distributed at each value of X • The variance is homogeneous (across X). • Observations are independent of each other and ei independent of the rest of the model. The regression of Y on X
The regression of Y on X (continued) • Special assumption for regression. • Assume that all of the variation is attributable to the dependent variable (Y), and that the variable X is measured WITHOUT ERROR. • Note that the deviations are measured vertically, not horizontally or perpendicular to the line.
Derivation of the formulas • Any observation can be written as • Yi = b0 + b1Xi + ei for a sample • where; ei = a deviation fo the observed point from the regression line • note, the idea of regression is to minimize the deviation of the observations from the regression line, this is called a Least Squares Fit
Derivation of the formulas (continued) • Sei = 0 • the sum of the squared deviations • Sei2 = S(Yi - Yhat)2 • Sei2 = S(Yi - b0 + b1Xi )2 • The objective is to select b0 and b1 such that Sei2 is a minimum, this is done with calculus • You do not need to know this derivation!
We have previously defined the uncorrected sum of squares and corrected sum of squares of a variable Yi • The uncorrected SS is SYi2 • The correction factor is (SYi)2/n • The corrected SS is SYi2 - (SYi)2/n • Your book calls this SYY, the correction factor is CYY • We could define the exact same series of calculations for Xi , and call it SXX A note on calculations
A note on calculations (continued) • We will also need a crossproduct for regression, and a corrected crossproduct • The crossproduct is XiYi • The Sum of crossproducts is SXiYi, which is uncorrected • The correction factor is (SXi)(SYi) / n = CXY • The corrected crossproduct is SXiYi-(SXi)(SYi)/n • Which you book calls SXY
Derivation of the formulas (continued) • the partial derivative is taken with respect to each of the parameters for b0
Derivation of the formulas (continued) • set the partial derivative to 0 and solve for b0 • 2 S(Yi-b0-b1Xi)(-1) = 0 • - SYi + nb0 + b1 SXi = 0 • nb0 = SYi - b1 SXi • b0 = `Y - b1`X • So b0 is estimated using b1 and the means of X and Y
Derivation of the formulas (continued) • Likewise for b1 we obtain the partial derivative
Derivation of the formulas (continued) • set the partial derivative to 0 and solve for b1 • 2 S(Yi-b0-b1Xi)(-Xi) = 0 • - S(YiXi + b0Xi + b1 Xi2) = 0 • -SYiXi + b0SXi + b1 SXi2) = 0 • and since b0 =`Y - b1`X ) , then • SYiXi = (SYi/n - b1 SXi/n )SXi + b1 SXi2 • SYiXi = SXiSYi/n - b1 (SXi)2/n + b1 SXi2 • SYiXi - SXiSYi/n = b1 [SXi2 - (SXi)2/n] • b1 = [SYiXi - SXiSYi/n] / [SXi2 - (SXi)2/n]
Derivation of the formulas (continued) • b1 = [SYiXi - SXiSYi/n] / [SXi2 - (SXi)2/n] • b1 = SXY / SXX • so b1 is the corrected crossproducts over the corrected SS of X • The intermediate statistics needed to solve all elements of a SLR are SXi, SYi, n, SXi2 , SYiXi and SYi2 (this last term we haven't seen in the calculations above, but we will need later)
Derivation of the formulas (continued) • Review • We want to fit the best possible line, we define this as the line that minimizes the vertically measured distances from the observed values to the fitted line. • The line that achieves this is defined by the equations • b0 = `Y - b1`X • b1 = [SYiXi - SXiSYi/n] / [SXi2 - (SXi)2/n]
Derivation of the formulas (continued) • These calculations provide us with two parameter estimates that we can then use to get the equation for the fitted line.
Numerical example • See Regression handout
Crossproducts are used in a number of related calculations. • a crossproduct = YiXi • Sum of crossproducts = SYiXi = SXY • Covariance = SYiXi / (n-1) • Slope = SXY / SXX • SSRegression = S2XY / SXX • Correlation = SXY / ÖSXXSYY • R2 = r2 = S2XY / SXXSYY = SSRegression/SSTotal About Crossproducts