Distributed Snapshot

1. Distributed Snapshot

2. -- How many messages are in transit on the internet? -- What is the global state of a distributed system of N processes? How do we compute these? Think about these

3. One-dollarbank Let a $1 coin circulate in a network of a million banks. How can someone count the total $ in circulation? If not counted “properly,” then one may think the total $ in circulation to be one million.

4. Major uses in - deadlock detection - termination detection - rollback recovery - global predicate computation Importance of snapshots

5. (a∈C) ⋀ (b ≺ a) ⇒b ∈ C If this is not true, then the cut C is inconsistent Consistent cut A cut is a set of events. If a cut C is consistent then time

6. Consistent snapshot The set of states immediately following the events (actions) in a consistent cut forms a consistent snapshot of a distributed system. • A snapshot that is of practical interest is the most recent one. Let C1 and C2 be two consistent cuts and C1⊂C2. Then C2 is more recent than C1. • Analyze why certain cuts in the one-dollar bank are inconsistent.

7. Consistent snapshot How to record a consistent snapshot? Note that 1. The recording must be non-invasive. 2. Recording must be done on-the-fly. You cannot stop the system.

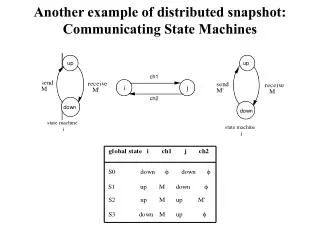
8. Works on a (1) strongly connected graph (2) each channel is FIFO. An initiator initiates the algorithm by sending out a marker ( ) Chandy-Lamport Algorithm

9. Initially every process is white. When a process receives a marker, it turns red if it has not already done so. Every action by a process, and every message sent by a process gets the color of that process. White and red processes

10. Step 1. In one atomic action, the initiator (a) Turns red (b) Records its own state (c) sends a marker along all outgoing channels Step 2. Every other process, upon receiving a marker for the first time (and before doing anything else) (a) Turns red (b) Records its own state (c) sends markers along all outgoing channels The algorithm terminates when (1) every process turns red, and (2) Every process has received a marker through each incoming channel. Two steps

11. Lemma 1. No red message is received in a white action. Why does it work?

12. Theorem. The global state recorded by Chandy-Lamport algorithm is equivalent to the ideal snapshot state SSS. Hint. A pair of actions (a, b) can be scheduled in any order, if there is no causal order between them, so (a; b) is equivalent to (b; a) Why does it work? All white All red SSS Easy conceptualization of the snapshot state

13. Why does it work? Let an observer observe the following actions: w[i] w[k] r[k] w[j] r[i] w[l] r[j] r[l] …  w[i] w[k] w[j] r[k] r[i] w[l] r[j] r[l] … [Lemma 1]  w[i] w[k] w[j] r[k] w[l] r[i] r[j] r[l] … [Lemma 1]  w[i] w[k] w[j] w[l] r[k] r[i] r[j] r[l] … [done!] Recorded state

14. Let us verify that Chandy-Lamport snapshot algorithm correctly counts the tokens circulating in the system Example 1: Count the tokens 2 token C token no token A no token token no token B A no token token no token C 1 3 B Are these consistent cuts? How to account for the channel states? Use sent and received variables for each process.

15. Example 2: Communicating State Machines

16. Something unusual Let machine i start Chandy-Lamport snapshot before it has sent M along ch1. Also, let machine j receive the marker after it sends out M’ along ch2. Observe that the snapshot state is down ∅ up M’ Doesn’t this appear strange? This state was never reached during the computation!

17. Understanding snapshot

18. Understanding snapshot The observed state is a feasible state that is reachable from the initial configuration. It may not actually be visited during a specific execution. The final state of the original computation is always reachable from the observed state.

19. Discussions What good is a snapshot if that state has never been visited by the system? - It is relevant for the detection of stable predicates. - Useful for checkpointing.

20. Discussions What if the channels are not FIFO? Study how Lai-Yang algorithm works. It does not use any marker LY1. The initiator records its own state. When it needs to send a message m to another process, it sends a message (m, red). LY2. When a process receives a message (m, red), it records its state if it has not already done so, and then accepts the message m. Question 1. Why will it work? Question 1 Are there any limitations of this approach?

21. Food for thought Distributed snapshot = distributed read. Distributed reset = distributed write How difficult is distributed reset?

22. Distributed debugging (Marzullo and Neiger, 1991) e, VC(e) observer Distributed system

23. Distributed debugging

24. Distributed debugging Possibly ϕ: At least one consistent global state S is reachable from the initial global state, such that φ(S) = true. Definitely ϕ: All computations pass through some consistent global state S such that φ(S) = true. Never ϕ: No computation passes through some consistent global state S such that φ(S) = true. Definitely ϕ ⇒Possibly ϕ

25. Examples ϕ = x+y =12 (true at S21) Possibly ϕ ϕ = x+y > 15 (true at S32) Definitely ϕ ϕ = x=y=5 (true at S40 and S22) Never ϕ *Neither S40 and S22 is a consistent state*

26. Global State Collection

27. Global state collection Some applications - computing network topology - termination detection - deadlock detection Chandy-Lamport algorithm does a partial job. Each process generates a fragment of the global state, but these pieces have to be “stitched together” to form a global state.

28. Once the pieces of a consistent global state become available, consider collecting the global state via all-to-all broadcast At the end, each process will compute a set V, where V= {s(i): 0 ≤ i ≤ N-1 } A simple exercise s(i) s(j) i j s(k) s(l) k l

29. All-to-all broadcast Assume that the topology is a strongly connected graph V.i W.i V.k W.k (i,k) (j,i) V.j W.j Acts like a “pump”