1 / 10

Understanding Exponential Functions and Half-Life in Radioactive Decay

Explore the concept of exponential functions, particularly focusing on half-life as a model for phenomena that decrease over time, such as radioactive decay. The half-life of a radioactive substance represents the time needed for half of it to decay to a non-radioactive state. For example, if a radioactive substance has a half-life of 14 days and starts with 6.6 grams, you can model the remaining quantity over time. This guide will explain how to express the amount remaining, calculate when only 1 gram will remain, and apply this knowledge through examples.

finola
Télécharger la présentation

Understanding Exponential Functions and Half-Life in Radioactive Decay

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

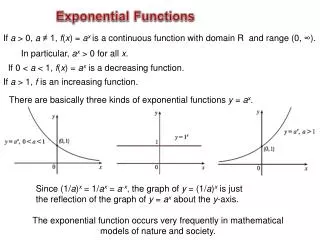
  1. 1.3 Exponential Functions

  2. Exponential Function

  3. Rules for Exponents

  4. Half-life Exponential functions can also model phenomena that produce decrease over time, such as happens with radioactive decay. The half-life of a radioactive substance is the amount of time it takes for half of the substance to change from its original radioactive state to a non-radioactive state by emitting energy in the form of radiation.

  5. Exponential Growth and Exponential Decay

  6. Ex: The half-life of a certain radioactive substance is 14 days. There are 6.6 g present initially.A. Express the amount of substance remaining as a function of time t.B. When will there be 1g remaining?

  7. The Number e

  8. The Number e

  9. Do example 5 on page 25

  10. Hwk: p. 26, 1-19 (odd), 21-39 (mults of 3)

More Related