1 / 14

Exponential Functions

This guide explores the fundamentals of exponential functions represented by f(x) = a * c^b(x-h) + k. We will analyze the roles of parameters a, b, and c, discussing how they affect vertical and horizontal stretches, initial values, and horizontal asymptotes. Additionally, we'll examine how the base influences the function's increase or decrease. Examples illustrate transformations and the identification of function characteristics. Join us in discovering the key elements that govern exponential functions and their applications.

palmer-duncan
Télécharger la présentation

Exponential Functions

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

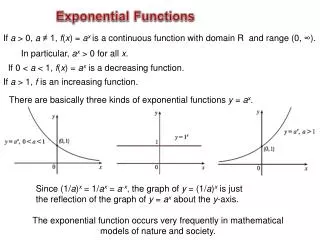
  1. Exponential Functions

  2. Basic Exponential Function f(x)=acbx exponential function in base c asymptote: x-axis a affects the vertical stretch a is also the initial value a can also flip the function b affects the horizontal stretch b is the period

  3. Role of the parameter “a” and “c” Where parameter b must always be positive!!! if c > 1 if 0 < c < 1 a > 0 a < 0

  4. Examples For each of the following, determine the base and indicate if the function is increasing or decreasing. Base = 3/4 Base = 3/2 Base = 3/2 Decreasing Decreasing Increasing

  5. Exponential Functions f(x)=acb(x-h) + k h shifts the initial value to the right or left k shifts the initial value up or down k is the horizontal asymptote

  6. Exponential Functions The rule f(x)=acb(x-h) + k can be re-written in the form: f(x)=acx + k where the function passes through the point (0, a + k) and has y = k as its asymptote

  7. Example Convert to the form f(x)=acx + k f(x) = 5(3)2(x+1) + 7 f(x) = 5(32) (x+1) + 7 f(x) = 5(9)(x+1) + 7 f(x) = 5(9x.91)+ 7 f(x) = 45(9x)+ 7 f(x) = 45(9)x+ 7

  8. Example Convert to the form f(x)=acx + k f(x) = -3(2)3x+1 + 4 f(x) = -3(2)3(x+1/3) + 4 f(x) = -3(8)(x+1/3) + 4 f(x) = -3(8x.81/3)+ 4 f(x) = -3(8x.2)+ 4 f(x) = -6(8x)+ 4 f(x) = -6(8)x+ 4

  9. Example If the point A(2,9) belongs to the graph of an exponential function of the form y = cx, determine the rule 9 = c2 3 = c y = 3x

  10. Example If the points A(1,4) and B(2,12) belong to the graph of an exponential function of the form y = acx, determine the rule 4 = ac1 12 = ac2 4 = a 12 = a c1 c2 4 = 12 c1 c2 4c2 = 12 c1 4c = 12 c = 3

  11. Exponential Functions f(x)=acb(x-h) + k FINDING THE ZEROS Plug in y=0 and solve for x! y=5(3)x-2 – 15 0=5(3)x-2 – 15 15=5(3)x-2 15/5=(3)(x-2) 3=(3)(x-2) 1 = x-2 3=x

  12. Euler's Number • A special irrational base of the exponential function • has a value of 2.71828… • abbreviated as e Examples: y = ex y = 3(e)x-1 - 2 • y = ex

  13. Example √e(e2x-1)(ex)=√e3

More Related