1 / 10

Exploring Simple Rational Functions Graphing

Learn to graph simple rational functions, understand vertical and horizontal asymptotes, and interpret the branches of hyperbolas. Practice with examples and solve for domain and range. Try solving assignments for better understanding.

gage-macias
Télécharger la présentation

Exploring Simple Rational Functions Graphing

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 9.2 Graphing Simple Rational Functions (p. 540)

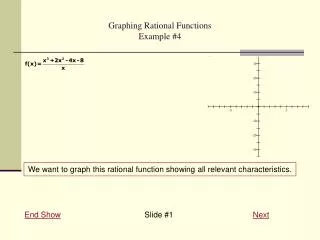
  2. Rational Function • A function of the form where p(x) & q(x) are polynomials and q(x)≠0.

  3. Hyperbola x=0 • A type of rational function. • Has 1 vertical asymptote and 1 horizontal asymptote. • Has 2 parts called branches. (blue parts) They are symmetrical. We’ll discuss 2 different forms. y=0

  4. Hyperbola (continued) • One form: • Has 2 asymptotes: x=h (vert.) and y=k (horiz.) • Graph 2 points on either side of the vertical asymptote. • Draw the branches.

  5. Hyperbola (continued) • Second form: • Vertical asymptote: Set the denominator equal to 0 and solve for x. • Horizontal asymptote: • Graph 2 points on either side of the vertical asymptote. Draw the 2 branches.

  6. Ex: Graph State the domain & range. Vertical Asymptote: x=1 Horizontal Asymptote: y=2 x y -5 1.5 -2 1 0 -1 4 3 Left of vert. asymp. Right of vert. asymp. Domain: all real #’s except 1. Range: all real #’s except 2.

  7. Ex: GraphState domain & range. Vertical asymptote: 3x+3=0 (set denominator =0) 3x=-3 x= -1 Horizontal Asymptote: x y -3 .83 -2 1.33 0 -.67 2 0 Domain: All real #’s except -1. Range: All real #’s except 1/3.

  8. You try! 

  9. You try! 

  10. Assignment543-544/12-39 mult. of 3

More Related