1 / 19

Mastering Trigonometric Identities with Mixed Expressions: A Comprehensive Guide

Explore the intricate world of trigonometric identities and learn how to manage expressions on both sides, including addition and multiplication. This lesson focuses on verifying identities through transformations using trig functions, symbols, and ratios while avoiding common pitfalls like dividing by zero. We emphasize effective strategies to handle complex expressions, such as starting with the side featuring addition. Engage with practice polls and student collaboration to solidify your understanding and develop problem-solving skills in preparing for the SAT.

ginger-franco
Télécharger la présentation

Mastering Trigonometric Identities with Mixed Expressions: A Comprehensive Guide

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

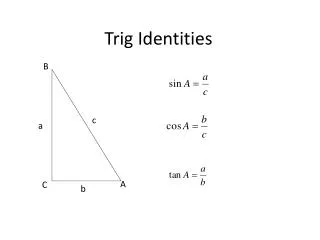
  1. Verifying Trig Identities (redux) Now we add mixed expressions on both sides (6.1)

  2. SAT Prep Quick poll! 1.

  3. SAT Prep Quick poll! 2.

  4. SAT Prep Quick poll! 3.

  5. POD Verify the identity.

  6. Review Trig expressions– contain symbols and ratios involving trig functions. The domain for each variable is that which makes the expression meaningful. (You can’t divide by 0.) We’ll use this more tomorrow, when we solve trig equations.

  7. Review Trig expressions– contain symbols and ratios involving trig functions. Use trig identities and algebra to 1. Transform either the left- or right-hand side into the other. 2. Transform both sides into a third equivalent expression. We do this through a series of reversible steps.

  8. Today So far, we’ve had a more complex side to transform into a simple expression. We now have mixed expressions on both sides. Generally speaking, we’ll still start with the more complex side.

  9. Try it If you have a choice between a side with addition and one with multiplication, start with the addition side.

  10. Try it If you have a choice between a side with addition and one with multiplication, start with the addition side.

  11. Try it Another with addition.

  12. Try it Another with addition.

  13. With double fractions Avoid cross multiplication– that can add extraneous solutions when we get to solving equations. Strategy here– start with the subtraction in the denominator.

  14. With double fractions Avoid cross multiplication. Strategy– start with the subtraction.

  15. With some, it’s a toss up Let’s work both sides on this one, and derive a third expression.

  16. With some, it’s a toss up We could work both sides on this one. Start with the left side

  17. With some, it’s a toss up Now, work the right side. Notice how this is the same expression as the one we derived from the left side.

  18. Student work A group of students was able to transform the left side into the right side.

  19. Student work Another group found a shorter way to work with the left side.

More Related