1 / 34

The subsitution Method

The substitution method is a powerful technique for solving complex integrals by transforming them into simpler forms. In this guide, we explore the fundamentals of the substitution method, beginning with an overview of indefinite integrals and antiderivatives. We illustrate the method through practical examples, including how to handle substitutions for difficult functions. The key is to identify a suitable substitution that simplifies the integral computation while maintaining accuracy. This resource is ideal for students seeking to deepen their understanding of integration techniques.

ishi
Télécharger la présentation

The subsitution Method

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. The subsitution Method Fatema Ahmed Alhajeri 201108382 #19

  2. Previous information an indefinite integral is a function ∫f(x)dx= F(x) where F’(x) = f(x) which represents a particular antiderivitive of f, or an entire family of antiderivitives.

  3. Example 1 ∫x √x dx = ∫ x x1/2 dx =∫ x (½ + 1) dx = ∫x 3/2dx Therefore using the intermediate integration rule:

  4. We can solve this previous equation: • F(x) = ∫ x3/2 dx • = (x5/2 ) + C 5/2 Therefore, • = F(x) = 2/5 x5/2+C

  5. The Substitution Method We need to use the substitution method in order to convert difficult equations, to fit the intermediate general equations in order to solve. Example 2 f(x) = ∫ 2x √(1+x2) dx = ∫ (1+x2 )1/2 2x dx Using substituion method we let u = 1+x2 since the derivitive of u (du) is = 2x and is present in the equation u = 1 +x2 du= 2x dx

  6. We now change the equation in terms of “u” where it equals to: • F (x)= ∫ (u)1/2 du • This equation fits the structure of: • Thus, • ∫ (u)1/2 du • = ∫ (u)3/2 + C 3/2 • = 2/3 u3/2 + C

  7. Now, replacing the “u” with the variable x to retrieve the final answer: = 2/3 √(1+x2)3/2 + C

  8. Chapter 5INTEGRALS THE SUBSITUTION RULE SomaiaElsherif 5.5 Math prject - Substitution rule

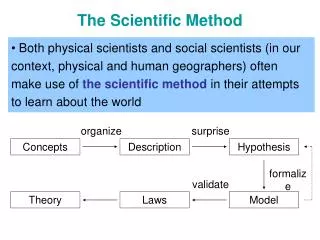
  9. The Substitution rule In general, Notice that each differentiation rule for functions provides a rule to find an antiderivative The substitution method is a rewriting method for integrals where we can extend the scope of these rules The idea behind substitution rule is to replace a relatively complicated integral by a simpler one Math prject - Substitution rule

  10. Summary of the substitution rule proof The Chain rule for differentiation The chain rule implies the substitution rule∫f’(g(x))g’(x) = f(g(x)) + C Substitution rule (according to text book) ∫ f(g(x))g’(x) dx = ∫ f(u) du where u = g(x), then du = g’(x) Math prject - Substitution rule

  11. The Substitution rule If u=g(x) is a differentiable function whose range is an interval I and f is continuous on I,Then ∫ f(g(x))g’(x) dx = ∫ f(u) du Notice that the rule was proved using the chain rule for differentiationThus, It is easy to remember it ! Only you have to think of dx and du in the previous formula as differentials Math prject - Substitution rule

  12. Example Find ∫ x³ cos (x⁴ + 2) dx. We made a substitution u = x⁴ + 2why? Because it’s differentiable function it’s differential is du = 4x³ dx, which, apart from the constant factor 4, occurs in the integral. Thus, using x³ dx = du/4 and the substitution rule we have Math prject - Substitution rule

  13. ∫x³ cos (x⁴ + 2) dx = ∫cos u . ¼ du = ¼ ∫ cos u du = ¼ sin u + C Notice that you have to return to the original variable x = ¼ sin (x⁴ + 2) + C Math prject - Substitution rule

  14. Notice that The main challenge in using the Substitution rule is to think of an appropriate substitution You have 2 ways to do it ! Choose u to be function in the integrand whose differential occurs ( except for a constant factor )this is similar to the previous example case Math prject - Substitution rule

  15. If the first method didn’t work, Try this Choose u to be some how complicated part of the integrand ( perhaps the inner function in a composite function ) Finally ! Finding the right substitution is a bit of art It’s not unusual to guess wrong If your first guess doesn’t work, just try another substitution Math prject - Substitution rule

  16. THE SUBSTITUTION RULE FOR DEFINITE INTEGRALS Done by: MahaMohd.Ibrahim. ID:201106851 Supervised by: Foud Al-muhannadi

  17. General rule If g’ is continuous on [a,b] and f is continuous on the range of u=g(x), then: =(

  18. Example Evaluate: To find the new limit of the integration we note that: When and when

  19. Therefore:

  20. Evaluate: Method (1):

  21. Method (2): ⇒ ⇒ The integral now is:

  22. We got the same answer!

  23. Definite integral :symmetry Gehaddesouky 201104686 #26

  24. Definite integral : symmetry We use the substitution by U to simplify the calculations of integrals of functions that are symmetric Example :

  25. Substitution rule (symmetry) The main rule is : If (F) is continues on [-a,a] if (f) is even then [f(-x)=f(X)], then If (F) is odd then [f(-x)=-f(X)], then

  26. Example 1, Evaluate by writing it As a sum of two integrals and interpreting one of those integrals in terms of an area.

  27. Example 2

  28. Thank you for your time

More Related