GE Proficy Historian Data Compression Introduction
260 likes | 350 Vues
Understand data compression methods used by GE Historian for efficient storage and retrieval. Learn about Collector Compression (CC) and Archive Compression (AC). Explore the benefits and considerations of data compression.

GE Proficy Historian Data Compression Introduction
E N D
Presentation Transcript
GE Proficy Historian Data Compression Introduction Stephen Friedenthal EVSystems www.evsystems.net sfriedenthal@evsystems.net
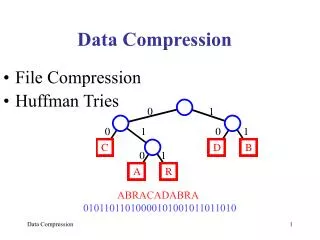
This method is used by the GE Historian What is data compression? • There are two fundamental classes of file compression: • Identify repeating elements (e.g., ZIP file compression) • Pros: No loss of information – all original data restored • Cons: CPU intensive – need to compress and decompress, large files take a lot of time • Identify redundant data that can be discarded (e.g., JPEG, dead-band, rate-of-change) • Pros: Fast, reduces network traffic, well suited for streaming data • Cons: Some data loss
Customer quotes when I ask them about compression? “Disk space is cheap.” “We don’t want to lose any data so we store everything” “Today’s computers are so fast there’s no penalty for storing everything.” “We’re a regulated industry…. We aren’t allowed to use compression.” From all of the above, you might come to believe that data compression is an antiquated response to a problem that no longer exists. Computers are fast, storage is cheap, so store everything.
Why compression is (still) important • “Needle in the haystack” problem • Much more difficult to find the truly interesting data • Limited network bandwidth • Storing terabytes of data is only useful if you can easily extract it • High long-term costs • Disk drives are “cheap”, but managing the data gets expensive • Superior performance • Storing the minimum necessary data greatly increases system performance and speed for clients & servers.
GE Historian Compression Methods • The Proficy Historian has two forms of data compression” • Collector compression (CC)—Also called, “dead band” compression. It works by examining data and discarding any that does not exceed a defined limit (e.g. +/- 0.5 Deg F.) • Archive Compression (AC)—Also called “rate of change” or “swinging door” compression. It works by examining data (after CC) and discarding any that falls within a slope range (more on this later.)
Stored sample Discarded samples x x x x x x x x x x Dead band x x x x x x Collector Compression Constant slope line • Collector compression overview • Pros: • Good at filtering out noise • Reduces data storage by 80 to ~90+% • Easy to understand • Cons: • Unable to reduce data when slope (vs. value) is unchanged (see constant slope section above)
Archive Compression • Archive compression looks at the data after collector compression • It only stores data that “changes direction” beyond a configured range • In effect, it stores data based on its rate of change. Compare to collector compression which stores data based on the amount of change.
Archive Compression Effect Red values are stored Green values are discarded Large change in slope, so values is stored Discarded by archive compression • Archive compression overview • Pros: • Can significantly reduce storage for certain signal types and noise • Stores only the most relevant values • Cons: • More difficult to tune • More difficult to understand
Archive Compression –A deeper dive How does it compare to OSI’s Swinging Door compression?
OSI PI Swinging Door Comrpession PI checks to see if all points lie inside the compression blanket, a dead band parallelogram drawn from end points using the CompDev as a tolerance. If any points fall outside the dead band, an archive event is triggered. Even though this is the point that falls outside the dead band, this is the one that gets archived because it is the last end point for which all points were inside the dead band.
Archive Compression vs. PI OSI PI swinging door algorithm checks if a point is inside parallelogram. The GE Historian algorithm checks if line between end points intersects the tolerance bar. 4) Check if ABS difference < CompDev 2) Calculate upper y for this x. 1) Calculate slope of upper line 3) Calculate difference 5) Check if point y is < upper y 6) Check if point y is > lower y 1) Calculate slope of this line 2) Calculate y for this x. 4) Calculate lower y for this x. 3) Calculate slope of lower line
GE Archive Compression vs. PI New Point Archived Point Swinging Door method. Instead of checking if each point is inside the parallelogram, the GE Proficy Historian checks if the line intersects the dead band of each point. GE Proficy Historian New Point Archived Point
GE Archive Compression Example • As an additional benefit, there is no need to buffer all points between the last archived point and the newest point. • Here’s an example of how it works. The key points to understand: • An “Archived Point” is one that is stored • A “Held Point” is the last good value that arrived. We don’t know if it will be stored until the next value arrives to tell us if the slope has changed sufficiently. Held Point Archived Point After a point is archived, the next point becomes the held point.
GE Archive Compression Example Construct error bands around the held point. PI: E = “CompDev” GE: E = deadband / 2 E E Archived Point Held Point
GE Archive Compression Example Step 1: Calculate the slopes of the two lines, U and L, connecting the archived point with the upper and lower ends of the error bands (dead band) associated with the held point. _ U _ L Archived Point Held Point
GE Archive Compression Example The upper and lower slopes define a critical aperture window. Critical Aperture Window _ U _ L Archived Point Held Point
GE Archive Compression Example If the slope of the line N, connecting the archived point with the new point, is between the upper and lower slopes, it intersects the dead band of the held point. _ U _ N New Point _ L Archived Point Held Point
GE Archive Compression Example • As new points are added, the previous new point becomes the current held point, and the same process is repeated. • The critical aperture window will always be constructed from the lowest upper slope and the highest lower slope to insure that the conditions necessary to compress all previous points will be preserved. • If the slope of the new point is within the critical aperture window, the previous held point may be discarded. You can forget about this point now. Forget the slope of this line New Point Remember the lowest upper slope and the highest lower slope. Held Point Forget the slope of this line
GE Archive Compression Example With each new point the process is continued, narrowing the aperture and discarding unnecessary points as you go. Forget Forget New Point Keep Held Point Forget
GE Archive Compression Example With each new point the process is continued, narrowing the aperture and discarding unnecessary points as you go. Keep Forget Forget New Point Held Point Forget
GE Archive Compression Example With each new point the process is continued, narrowing the aperture and discarding unnecessary points as you go. If this continues long enough, the critical aperture window will close, converging on the slope of the trend for this segment. Keep Forget Forget New Point Held Point Forget
GE Archive Compression Example When the slope of the new point lies outside of the critical aperture window, an archive event is triggered. Keep Outside critical aperture window. Forget New Point Forget Held Point Forget
GE Archive Compression Example The held point is archived, the new point becomes the held point and the process starts anew. The previous new point is now the held point. Held Point Archived Point The held point is now archived.
GE Archive Compression Example The process continues, as additional data arrive the critical aperture grows longer and thinner until a new value triggers an archive event. Held Point
GE Archive Compression Example This one example is very encouraging, but more statistically significant work must be done as well as a data quality assessment comparing these approaches. 23 out of 120 points archived 10 out of 120 points archived
Questions Stephen Friedenthal EVSystems www.evsystems.net 617.916.5101