Assembly line balancing

1. Dr. Ron Lembke Assembly line balancing

2. Situation: Assembly-line production. Many tasks must be performed, and the sequence is flexible Parts at each station same time Tasks take different amounts of time How to give everyone enough, but not too much work for the limited time. Assembly-Line Balancing

3. Product-Oriented Layout Operations BeltConveyor

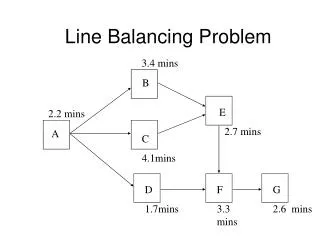
4. Draw precedence graph (times in minutes) Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

5. Ok: AC|BD|EG|FH|IJ • ABG|CDE|FHI|J C|ADB|FG|EHI|J • NOT ok: BAG|DCH|EFJ|I • DAC|HFE|GBJ|I Legal arrangements B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

6. AC|BD|EG|FH|IJ = max(25,15,23,15,19) = 25 ABG|CDE|FHI|J = max(40,23,27,7) = 40 C|ADB|FG|EHI|J = max(5,35,18,32,7) = 35 Legal arrangements CT = maximum of workstation times B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3 AC BD EG FH IJ

7. Production Time in each day C = Required output per day (in units) The more units you want to produce per hour, the less time a part can spend at each station. Cycle time = time spent at each spot C = 800 min / 32 = 25 min 800 min = 13:20 Cycle Time

8. Sum of task times (T) Nt = Cycle Time (C) Given required cycle time, find out the theoretical minimum number of stations Nt = 97 / 25 = 3.88 = 4 (must round up) Number of Workstations

9. Assign tasks by choosing tasks: • with largest number of following tasks • OR by longest time to complete Break ties by using the other rule Assignments

10. Nodes# after C 6 D 5 A 4 B,E,F 3 G,H 2 I 1 Number of Following Tasks Choose C first, then, if possible, add D to it, then A, if possible. B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

11. Draw precedence graph (times in seconds) Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

12. Nodes# after A 4 B,E,F 3 G,H 2 I 1 Number of Following Tasks A could not be added to first station, so a new station must be created with A. B, E, F all have 3 stations after, so use tiebreaker rule: time. B = 5 E = 8 F = 3 Use E, then B, then F. B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

13. E cannot be added to A, but E can be added to C&D. Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

14. Next priority B can be added to A. Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

15. Next priority B can be added to A. Next priority F can’t be added to either. Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

16. Nodes# after G,H 2 I 1 Number of Following Tasks G and H tie on number coming after. G takes 15, H is 12, so G goes first.

17. G can be added to F. H cannot be added. Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

18. I is next, and can be added to H, but J cannot be added also. Precedence Diagram B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

19. Why not put J with F&G? Precedence Requirements B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3 AB CDE HI FG J

20. We know that at least 4 workstations will be needed. We needed 5. = 97 / ( 5 * 25 ) = 0.776 We are paying for 125 minutes of work, where it only takes 97. Calculate Efficiency Sum of task times (T) Efficiencyt = Actual # WS * Cycle Time

21. Try choosing longest activities first. A is first, then G, which can’t be added to A. Longest first B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

22. H and I both take 12, but H has more coming after it, then add I. Longest first B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

23. D is next. We could combine it with G, which we’ll do later. E is next, so for now combine D&E, but we could have combined E&G. We’ll also try that later. Longest first B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

24. J is next, all alone, followed by C and B. Longest first B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

25. F is last. We end up with 5 workstations. Longest first B A G 5 20 15 E I J C 8 D 7 12 H 3 CT = 25, so efficiency is again Eff = 97/(5*25) = 0.776 F 5 10 12

26. Go back and try combining G and E instead of D and E. Longest first- combine E&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

27. J is next, all alone. C is added to D, and B is added to A. Longest first- combine E&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

28. F can be added to C&D. Five WS again. CT is again 25, so efficiency is again 0.776 Longest first- combine E&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

29. Back up and combine D&G. No precedence violation. LONGEST FIRST - COMBINE D&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

30. Unhook H&I so J isn’t stranded again, I&J is 19, that’s better than 7. E&H get us to 20. This is feeling better, maybe? LONGEST FIRST - COMBINE D&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

31. 5 Again! CT is again 25, so efficiency is again 97/(5*25) = 0.776 LONGEST FIRST - COMBINE D&G B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

32. Can we do better? B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

33. If we have to use 5 stations, we can get a solution with CT = 20. Can we do better? B A G 5 20 15 E I J C 8 D 7 12 H F 5 10 12 3

34. With 5 WS at CT = 20 = 97 / ( 5 * 20 ) = 0.97 We are paying for 100 minutes of work, where it only takes 97. Calculate Efficiency Sum of task times (T) Efficiencyt = Actual # WS * Cycle Time

35. With 20 min CT, and 800 minute workday • Output = 800 min / 20 min/unit = 40 units • Don’t need to work 800 min • Goal 32 units: 32 * 20 = 640 min/day • 5 workers * 640 min = 3,200 labor min. • We were trying to achieve • 4 stations * 800 min = 3,200 labor min. • Same labor cost, but more workers on shorter workday Output and Labor Costs

36. Long tasks make it hard to get efficient combinations. • Consider splitting tasks, if physically possible. • If not: • Parallel workstations • use skilled (faster) worker to speed up Handling Long Tasks

37. Compute desired cycle time, based on Market Demand, and total time of work needed • Methods to use: • Largest first, most following steps, trial and error • Compute efficiency of solutions • A shorter CT can sometimes lead to greater efficiencies • Changing CT affected length of work day, looked at labor costs Summary