Time Series Analysis

1. Time Series Analysis

2. “Forecasting is very dangerous, especially about the future.” --- Samuel Goldwyn

3. Introduction to Time Series Analysis • A time-series is a set of observations on a quantitative variable collected over time. • Examples • Dow Jones Industrial Averages • Historical data on sales, inventory, customer counts, interest rates, costs, etc • Businesses are often very interested in forecasting time series variables. • Often, independent variables are not available to build a regression model of a time series variable. • In time series analysis, we analyze the past behavior of a variable in order to predict its future behavior.

4. Good forecasts can lead to • Reduced inventory costs. • Lower overall personnel costs. • Increased customer satisfaction. • The Forecasting process can be based on • Educated guess. • Expert opinions. • Past history of data values, known as a time series.

5. Forecasting is fundamental to decision-making. There are three main methods: • Subjective forecasting is based on experience, intuition, guesswork and a good supply of envelope-backs. • Extrapolation is forecasting with a rule where past trends are simply projected into the future. • Causal modeling (cause and effect) uses established relationships to predict, for example, sales on the basis of advertising or prices.

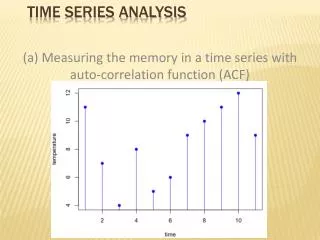
6. Some Time Series Terms • Stationary Data - a time series variable exhibiting no significant upward or downward trend over time. • Nonstationary Data - a time series variable exhibiting a significant upward or downward trend over time. • Seasonal Data - a time series variable exhibiting a repeating patterns at regular intervals over time.

7. Stationarity

8. Non-stationarity (upward trend)

9. Components of a Time Series • Long Term Trend • A time series may be stationary or exhibit trend over time. • Long term trend is typically modeled as a linear, quadratic or exponential function. • Seasonal Variation • When a repetitive pattern is observed over some time horizon, the series is said to have seasonal behavior. • Seasonal effects are usually associated with calendar or climatic changes. • Seasonal variation is frequently tied to yearly cycles. • Cyclical Variation • An upturn or downturn not tied to seasonal variation. • Usually results from changes in economic conditions. • Random effects

10. The Trend Component The long-term tendency is usually one of three: growth, decline, or constant. Reasons for trends include: Population growth -- greater demand for products and services -- greater supply of products and services Technology -- impacts on efficiency, supply, and demand Innovation -- impacts efficiency as well as supply and demand

11. The Seasonal Component Upward and downward movements which repeat at the same time each year. Reasons for seasonal influences include: Weather -- both outdoor and indoor activities can impact demand because of the number of people involved -- supplies of products and services may depend on the weather Events, Holidays -- often impact supply and demand

12. The Cyclical Component Similar to seasonal variations except that there is likely not a relationship to the time of the year. Examples of cyclical influences include: Inflation/deflation -- energy costs, wages and salaries, and government spending Stock market prices -- bull markets, bear markets Consequences of unique events -- severe weather, law suits

13. The Irregular Component Unexplained variations which we usually treat as randomness. This is the equivalent of the error term in the analysis of variance model and the regression model. These are short-term effects, usually. We treat them as independent from one time period to the next. The length of the duration of these effects would then be shorter than one time period, that is, one month for monthly data, one year for annual data.

14. Time-Series Model • The four components of time series come together to form a time series model. • There are two popular time series models: • Additive Model: • Multiplicative Model: Where Tt is the trend, St is the seasonal, Ct is the cyclical and It is the irregular component.

15. Typical Time Series patterns Non linear trend time series Linear trend time series Linear Trend and Seasonality time series A Stationary Time Series

16. Approaching Time Series Analysis • There are many, many different time series techniques. • It is usually impossible to know which technique will be best for a particular data set. • It is customary to try out several different techniques and select the one that seems to work best. • To be an effective time series modeler, you need to keep several time series techniques in your “tool box.”

17. Measuring Accuracy • We need a way to compare different time series techniques for a given data set. • Four common techniques are the: • mean absolute deviation, • mean absolute percent error, • the mean square error, • root mean square error. We will focus on the MSE.

18. Extrapolation Models • Extrapolation models try to account for the past behavior of a time series variable in an effort to predict the future behavior of the variable. • We’ll first talk about several extrapolation techniques that are appropriate for stationary data.

19. An Example • Electra-City is a retail store that sells audio and video equipment for the home and car. • Each month the manager of the store must order merchandise from a distant warehouse. • Currently, the manager is trying to estimate how many VCRs the store is likely to sell in the next month. • He has collected 24 months of data.

20. Moving Averages • No general method exists for determining k. • We must try out several k values to see what works best.

21. A Comment on Comparing MSE Values • Care should be taken when comparing MSE values of two different forecasting techniques. • The lowest MSE may result from a technique that fits older values very well but fits recent values poorly. • It is sometimes wise to compute the MSE using only the most recent values.

22. Forecasting With The Moving Average Model Forecasts for time periods 25 and 26 at time period 24:

23. The weighted moving average technique allows for different weights to be assigned to previous observations. Weighted Moving Average • The moving average technique assigns equal weight to all previous observations • We must determine values forkand thewi

24. Forecasting With The Weighted Moving Average Model Forecasts for time periods 25 and 26 at time period 24:

25. It can be shown that the above equation is equivalent to: Exponential Smoothing

26. Examples of TwoExponential Smoothing Functions

27. Forecasting With The Exponential Smoothing Model Forecasts for time periods 25 and 26 at time period 24: Note that,

28. Seasonality • Seasonality is a regular, repeating pattern in time series data. • May be additive or multiplicative in nature...

29. Stationary Seasonal Effects

31. Seasonal Variation

32. Stationary Data With Additive Seasonal Effects • Et is the expected level at time period t. • St is the seasonal factor for time period t. where prepresents the number of seasonal periods

33. Forecasting With The AdditiveSeasonal Effects Model Forecasts for time periods 25 to 28 at time period 24:

34. Stationary Data With Multiplicative Seasonal Effects • Et is the expected level at time period t. • St is the seasonal factor for time period t. where p represents the number of seasonal periods

35. Forecasting With The MultiplicativeSeasonal Effects Model Forecasts for time periods 25 to 28 at time period 24:

36. Trend Models • Trend is the long-term sweep or general direction of movement in a time series. • We’ll now consider some nonstationary time series techniques that are appropriate for data exhibiting upward or downward trends.

37. An Example • WaterCraft Inc. is a manufacturer of personal water crafts (also known as jet skis). • The company has enjoyed a fairly steady growth in sales of its products. • The officers of the company are preparing sales and manufacturing plans for the coming year. • Forecasts are needed of the level of sales that the company expects to achieve each quarter. • See file Fig11-19.xls

38. Double Moving Average where • Etis the expected base level at time periodt. • Ttis the expected trend at time periodt.

39. Forecasting With The Double Moving Average Model Forecasts for time periods 21 to 24 at time period 20:

40. where Et = aYt + (1-a)(Et-1+ Tt-1) Tt = b(Et -Et-1) + (1-b) Tt-1 Double Exponential Smoothing(Holt’s Method) • Etis the expected base level at time periodt. • Ttis the expected trend at time periodt.

41. Forecasting With Holt’s Model Forecasts for time periods 21 to 24 at time period 20:

42. Holt-Winter’s Method For Additive Seasonal Effects where

43. Forecasting With Holt-Winter’s Additive Seasonal Effects Method Forecasts for time periods 21 to 24 at time period 20:

44. Holt-Winter’s Method For Multiplicative Seasonal Effects where

45. Forecasting With Holt-Winter’s Multiplicative Seasonal Effects Method Forecasts for time periods 21 to 24 at time period 20:

46. The Linear Trend Model For example:

47. Forecasting With The Linear Trend Model Forecasts for time periods 21 to 24 at time period 20:

48. The TREND() Function TREND(Y-range, X-range, X-value for prediction) where: Y-range is the spreadsheet range containing the dependent Y variable, X-range is the spreadsheet range containing the independent X variable(s), X-value for prediction is a cell (or cells) containing the values for the independent X variable(s) for which we want an estimated value of Y. Note: The TREND( ) function is dynamically updated whenever any inputs to the function change. However, it does not provide the statistical information provided by the regression tool. It is best two use these two different approaches to doing regression in conjunction with one another.

49. The Quadratic Trend Model

50. Forecasting With The Quadratic Trend Model Forecasts for time periods 21 to 24 at time period 20: