1 / 20

Lecture 6: Framing and Error Detection-Data Link Layer Functions

This lecture focuses on the Data Link Layer functions, reviewing key concepts relating to framing and error detection as introduced in previous lectures. It discusses the importance of reliable data transmission over a single link and explores various framing techniques, including bit-oriented and byte-oriented approaches. Error detection methods such as Cyclic Redundancy Check (CRC) and two-dimensional parity are thoroughly examined, with emphasis on polynomial operations for error checking. This comprehensive review equips you with the knowledge needed to understand and implement data link layer protocols effectively.

mulan
Télécharger la présentation

Lecture 6: Framing and Error Detection-Data Link Layer Functions

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Lecture 6: Framing and Error Detection-Data Link Layer Functions

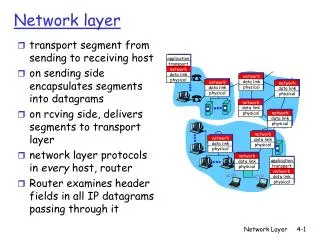
  2. Review of Lecture 5 • Level 1: Physical or Hardware Layer • Deals with the transmission of bits • Signal Generation and Modulation • Encoding • Implemented by adapters and device drivers

  3. Review of Lecture 5 • Level 2: Data Link Layer • Deals with reliable transmission of data over a single link (does not include routing over a network of links) • Framing • Error Detection

  4. 8 16 16 8 Beginning Ending Header Body CRC sequence sequence Review of Lecture 5 • Last time—Bit oriented protocol with sentinel strings (01111110 at beginning and end of frame • Uses bit-stuffing to identify sentinel strings in the payload • Sender inserts zero after string of five 1’s • Receiver deletes stuffed bits

  5. Byte oriented framing-Byte counting approach • include payload length in header • e.g., Digital Data Communication Message Protocol (DDCMP) • problem: count field corrupted • solution: catch when CRC fails

  6. Byte-oriented framing: Sentinel Approach DLE character precedes ETX within the body

  7. Clock-based framing • SONET: Synchronous Optical Network • each frame is 125us long • STS-n (STS-1 = 51.84 Mbps)

  8. Error Detection and Correction • Two dimensional Parity • Cyclic Redundency Check • Internet checksum

  9. Two Dimensional Parity Detects and corrects single bit errors Detects 2 and 3 bit errors Fails for 4 errors at the corners of box

  10. 8 16 16 8 Beginning Ending Header Body CRC sequence sequence Cyclic Redundancy Check • Add k bits of extra data (the CRC field) to an n-bit message to provide error detection function • For efficiency, want k << n • e.g., k = 32 for Ethernet and n = 12,000 (1500 bytes)

  11. Polynomials with binary coefficients • Represent n-bit message as n-1 degree polynomial • e.g., MSG=10011010 as M(x) = x7 + x4 + x3 + x1 • Addition (no carry) Subtraction (no borrow) • 10011010 00101110 10110100 10110100 • 00101110 10011010 • A-B=AXORB

  12. Polynomials with binary coefficients • Multiplication 1110 The usual 1110 without 11100 carrying 1110 1110 1010100

  13. Polynomials with binary coefficients • Division 1110 The usual 1110÷1010100 without the 1110 borrowing 1001 1110 1110 1110 0

  14. CRC strategy • Sender and Receiver know the “divisor polynomial” • e.g. C(x)=x3+x2+1=1101 • Send Message÷ CRC with CRC chosen so that the whole thing is evenly divisible by C(x) • Receiver calculates the remainder of Message÷ CRC/C(x) There’s an error if it is not zero

  15. CRC example • Message=10011010 C=1101(3 rd order) • Message÷ CRC=10011010XYZ • Choose XYZ so that remainder is zero for Message÷ CRC/C

  16. CRC Example cont. • 11111001 1101÷10011010XYZ1101 1001 1101 1000 1101 X=1 1011 Y=0 1101 Z=1 1100 1101 1xyz 1101 • Message÷ CRC=10011010÷ 101

  17. CRC Example cont. • 11111001 1101÷10011010000 1101 1001 1101 1000 1101 1011 1101 1100 1101 1000 1101 101 • Message÷ CRC=10011010000 - (xor) 101

  18. CRC (cont) • Let k be the degree of some divisor polynomial • e.g., C(x) = x3 + x2 + 1 • Transmit polynomial P(x) that is evenly divisible by C(x) • shift left k bits, i.e., M(x)xk • subtract remainder of M(x)xk / C(x) from M(x)xk • Receiver polynomial P(x) + E(x) • E(x) = 0 implies no errors • Divide (P(x) + E(x)) by C(x); remainder zero if: • E(x) was zero (no error), or • E(x) is exactly divisible by C(x) (unlikely for CRC-32)

  19. Selecting C(x) • All single-bit errors, as long as the xk and x0 terms have non-zero coefficients. • All double-bit errors, as long as C(x) contains a factor with at least three terms • Any odd number of errors, as long as C(x) contains the factor (x + 1) • Any ‘burst’ error (i.e., sequence of consecutive error bits) for which the length of the burst is less than k bits. • Most burst errors of larger than k bits can also be detected • See Table 2.6 on page 102 for common C(x)

  20. Internet Checksum Algorithm • View message as a sequence of 16-bit integers; sum using 16-bit ones-complement arithmetic; take ones-complement of the result. u_short cksum(u_short *buf, int count) { register u_long sum = 0; while (count--) { sum += *buf++; if (sum & 0xFFFF0000) { /* carry occurred, so wrap around */ sum &= 0xFFFF; sum++; } } return ~(sum & 0xFFFF); }

More Related