Performance

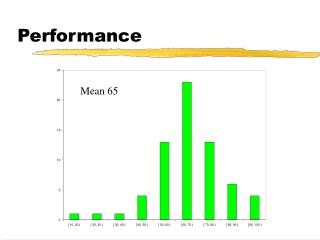
1. Performance Mean 65

2. Solutions to Exam 2 • We have a single commodity in warehouses around the country and wish to ship it to our customers at minimum cost. The carrier charges us a cost per unit shipped that depends only on the location of the warehouse and the location of the customer. • Transportation Model

3. Weight & Cube • We have several commodities in warehouses around the country and wish to ship them to our customers at minimum cost. The commodities have different unit weights and densities. The carrier charges us a cost per truck load shipped that depends only on the location of the warehouse and the location of the customer. The truck has both a weight limit and a cubic capacity. If we ship a truck that is only partially full, the carrier will charge us for the larger of the fraction of the weight limit of the truck that we use or the fraction of the cubic capacity of the truck that we use. General Linear Programming Model

4. Single Sourcing • We have a single commodity in warehouses around the country and wish to ship it to our customers at minimum cost. The carrier charges us a cost per unit shipped that depends only on the location of the warehouse and the location of the customer. Each customer insists on receiving all of his demand from a single warehouse. Different customers may be served from different warehouses, but no customer can be served by more than one warehouse. • General Mixed Integer Linear Programming Model

5. Sets and Parameters • /* The Plants */ • set PLANTS; • /* The DCS */ • set DCS; • /* The Cross Docks */ • set CROSSDOCKS; • /* The capacity at each plant */ • param Capacity{PLANTS}; • /* The Demand at each Cross Dock */ • param Demand{CROSSDOCKS};

6. Variables and Objective • /* The set of shipments possible */ • set EDGES := (PLANTS cross DCS) union (DCS cross CROSSDOCKS); • /* The unit cost on each edge */ • param Cost{EDGES}; • /* The variables are the quantities shipped on each edge */ • var Ship{EDGES} >= 0; • /* The Objective: Minimize Freight Costs */ • minimize FreightCost: • sum{(f,t) in EDGES} Cost[f,t]*Ship[f,t];

7. Constraints • /* Constraints: Observe plant capacities */ • s.t. PlantCapacities {plant in PLANTS}: • sum{(plant, dc) in EDGES} Ship[plant, dc] <= Capacity[plant]; • /* Constraints: Meet Demand at each CROSSDOCK */ • s.t. MeetDemand{dock in CROSSDOCKS} • sum{(dc,dock) in EDGES} Ship[dc,dock] >= Demand[dock]; • /* Constraints: Conserve Flow at DC's */ • s.t. ConserveFlow{dc in DCS} • sum {(plan, dc) in EDGES} Ship[plant, dc] • = sum {(dc, dock) in EDGES} Ship[dc, dock];

8. Single Sourcing etc • The model described above does not impose the single sourcing constraints at the DCs or the single destination for the plants. Here’s how to do that -- merge the following with the previous model • /* Whether or not we use each edge */ var UseEdge{EDGES} binary; s.t. DefineUseEdgePlant{(plant, dc) in EDGES: plant in PLANTS}: Ship[plant, dc] <= Capacity[plant]*UseEdge[plant,dc]; s.t. DefineUseEdgeDock{(dc, dock) in EDGES: dock in CROSSDOCKS}: Ship[dc, dock] <= Demand[dock]*UseEdge[dc, dock];

9. Single Sourcing etc. /* Use one edge from each plant */ s.t. SingleDCforPlant {plant in PLANTS}: sum{dc in DCS} UseEdge[plant,dc] = 1; /* Use one edge to each Cross Dock */ s.t. SingleDCforCrossDock{dock in CROSSDOCKS}: sum{dc in DCS} UseEdge[dc, dock] = 1;

10. Building the System • Disney is planning to build tunnels to connect its merchandise warehouse in EuroDisney to all of the stores in the park. For safety reasons, the company will not allow tunnels to connect except at the warehouse or at stores. It wishes to minimize the cost of building the tunnels. • Minimum Spanning Tree Model

11. Using the System • After the tunnels (described in d.) are built, Disney is concerned with getting special orders to the stores from the warehouse as quickly as possible using a combination of the tunnels and surface streets. It has estimates of the time required to travel through each tunnel and down each street. • Shortest Path Model

12. Formulation • Pratt & Whitney is preparing to make final arrangements for delivery of jet engines from its final assembly plants to aircraft manufacturers’ sites. • Each jet engine is transported in a 747. A 747 can carry only a single engine at a time. • Each engine costs $100 million. Pratt & Whitney estimates inventory carrying cost at about 25%/year.

13. P & W Formulation • The set of P&W Plants • set PLANTS; • The set of customer manufacturing sites • set SITES; • The capacities of the plants in engines per year • param Capacity{PLANTS}; • The demands at the customer manufacturing sites in engines per year • param Demand{SITES};

14. The freight cost per engine from each plant to each customer site • param FreightCost{PLANTS, SITES}; • The travel time in days from each plant to each customer site • param TravelDays{PLANTS, SITES}; • The Engine Cost in $/engine • param EngineCost; • The inventory carrying cost as a fraction of the value of the item charged per year • param HoldingCost;

15. The Heart of the Matter • Calculated parameter, the freight and inventory cost incurred per engine shipped from each plant to each site in $/engine • param Cost{plant in PLANTS, site in SITES} • := FreightCost[plant, site] + • HoldingCost*EngineCost* • TravelDays[plant, site]/365;

16. The Model • Variables: Number of engines shipped from each plant to each customer manufacturing site • This is a transportation problem (with integer data) so we don't need to specify that these variables be integral. • var Ship{PLANTS, SITES} >= 0;

17. The Model • Objective: Minimize annual freight and pipeline inventory costs minimize TotalCost: sum{plant in PLANTS, site in SITES} Cost[plant, site]*Ship[plant, site]; s.t. ObserveCapacity {plant in PLANTS}: sum{site in SITES} Ship[plant, site] <= Capacity[plant]; s.t. MeetDemand{site in SITES}: sum{plant in PLANTS} Ship[plant, site] >= Demand[site];

18. Set Covering/Location • Intel Corporation is facing increasing pressure to provide consignment inventory to computer manufacturers in emerging markets including Eastern Europe. The company has 10 major customers in the region and holds options to lease at 5 sites in the region. It would like to exercise the fewest options necessary to guarantee it has a warehouse within 200 miles of each customer. • Formulate an optimization model to identify which lease options Intel should exercise in order to ensure it has the fewest possible warehouses and has a warehouse within 200 miles of each customer.

19. The set of Intel Sites • set SITES; • The set of Customer Sites • set CUSTS; • The distance data • param Dist{SITES, CUSTS}; • The allowed distance (200 miles) • param MaxDist;

20. Calculated parameter: is customer within 200 miles of the site? • Param Covers{site in SITES, cust in CUSTS} • := if Dist[site,cuts] < MaxDist • then 1 else 0; • Variables: Open the site or not • var Open{SITES} binary;

21. The Model • Objective: Minimize the number of sites opened • miminize OpenSites: • sum {site in SITES} Open[site]; • s.t. CoverEachCustomer{cust in CUSTS} • sum{site in SITES} Covers[site, cust]*Open[site] • >= 1;

22. set PRODUCERS; • set PRODUCTS; • set PORTS; • set DCS; • set CROSSDOCKS; • param Supply{PRODUCERS, PRODUCTS}; • param Demand{CROSSDOCKS, PRODUCTS};

23. set EDGES dimen 2; • param Cost{EDGES}; • var Flow{EDGES, PRODUCTS}>=0; • minimize FreightCost: • sum{(f,t) in EDGES, prd in PRODUCTS} Cost[f,t]*Flow[f,t,prd];

24. s.t. RespectSupply{producer in PRODUCERS, • prd in PRODUCTS}: • sum{(producer, t) in EDGES, prd in PRODUCTS} • Flow[producer, t, prd] • <= Supply[producer, prd]; • s.t. MeetDemand{crossdock in CROSSDOCKS, • prd in PRODUCTS}: • sum{(f, crossdock) in EDGES, prd in PRODUCTS} • Flow[f, crossdock, prd] • >= Demand[crossdock, prd];

25. The Problem • s.t. ConserveFlow{fac in PORTS union DCS}: • sum{(f, fac) in EDGES, • prd in PRODUCTS} Flow[f, fac, prd] • = sum{(fac, t) in EDGES, • prd in PRODUCTS} Flow[fac, t, prd];