Variable Population Size
150 likes | 333 Vues
Variable Population Size. Generalized Rastrigin Environment. Common Parameters. Evolve for 1000 generations Tournament Selection, s=2 Each gene’s initial sigma calculated as: n =number of dimensions, p vol =hypervolume of problem=10.24 n , coeff =10.0

Variable Population Size
E N D
Presentation Transcript
Variable Population Size Generalized Rastrigin Environment
Common Parameters • Evolve for 1000 generations • Tournament Selection, s=2 • Each gene’s initial sigma calculated as:n=number of dimensions, pvol=hypervolume of problem=10.24n, coeff=10.0 • Each genes tau is set to 0.05*(initial sigma) • Mutation rate = 1.0 • every child’s gene mutated • Crossover Rate = 0.0 • No crossover at this point
“Greedy” Parameters • Population Size = 50 • Elitism rate = 0.5 • On average, half of population is cloned into next generation, chosen via tournament selection • Asexual Reproduction Rate is 0.5 • On average, half of individuals in population produce one child via mutation, chosen via tournament selection
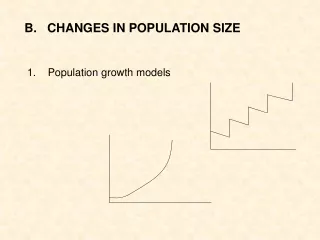
Variable Population Size Parameters • Initial Population Size = 50 • Elitism Rate is 1.0 • Every individual is cloned to the next generation • Asexual Reproduction Rate is 1.0 • On average, every individual produces one child via mutation, chosen via tournament selection • Selection Event periodicity is 5 generations • Given the above two parameters, the population size doubles every generation. To compensate, every 5 generations, tournament selection is used to trim the population back down to the initial size.
Generalized Rastrigin Environment • A commonly used benchmark function for genetic algorithms, it provides many suboptimal local minima, and a single global minima at the origin.
Comments • 3D • Average fitness of population converges to solution….good or bad? Good in that we know this is the solution; bad in that could this allow for premature convergence? I think this depends on your excellent “coverage” idea. • 4D • Less of an impact on solution performance than expected. • One thing to note that is common throughout these simulations is that the best fitness continues to improve throughout the run for the variable population size setup, but not for the “Greedy” one. • 5D and 6D • The above point is particularly emphasized on the 5D problem. • Note the average fitness continually moving in the “correct” direction; not the case for “Greedy”.
Arguments/Defense • Argument: this variable population size problem has a greater average population size than the “Greedy” algorithm, which explains why it works better. • Try the “Greedy” algorithm with a larger population size to compensate. • The average of the “Variable” algorithm outlined here is avg(50, 100, 200, 400, 800) = 310 • Try the “Greedy” algorithm with a longer timespan to compensate.
Arguments/Defense • Try the “Greedy” algorithm with a larger population size to compensate. • Same average population size (310) • Performance improved, still not as good in the same timespan, especially when considering average fitness • Same maximum population size (800) • Performance improved, curiously not as much as it was for the previous case. Most likely an effect of only running a single experiment. • Try the “Greedy” algorithm with a longer timespan to compensate. • No discernable effect on performance.