Understanding MD5 Collision Attacks: Techniques and Probabilities
210 likes | 322 Vues
Explore the intricacies of MD5 hash function collisions, differential cryptanalysis, and attack techniques. Learn how non-linear functions and round differentials play a role in finding collisions efficiently.

Understanding MD5 Collision Attacks: Techniques and Probabilities
E N D
Presentation Transcript
MD5 Collisions Isabelle Stanton Chalermpong Worawannotai
Description of MD5 • Takes any message and outputs an 128-bit hash. • A message is padded so the length is a multiple of 512 by concatenating a 1 then 0’s and it’s length as a 64 bit number. • Each 512 bit block is compressed individually
Continued Description • The 512-bit block is divided into 16 32-bit words • There are 4 32-bit registers a, b, c and d. These are initially loaded with IV0 and carry the hash values from one 512-bit block to the next • It works in an iterative (chaining) process: Hi+1 = f(Hi,Mi) IV0=H0 where Mi is a 512 bit block.
Hash Chaining M1 M2 Mn … f f f H0=IV0 fixed Hn = H H2 H1 Mi 512 bits Hi 128 bits
One small step • For each f there are 4 rounds and each round has 16 steps • Ti and Si are fixed constant and depend only on the steps. Courtesy of www.wikipedia.org
The Rounds • Mi=(w0,…,w15) • For fixed i, 4 consecutive steps will yield ai+4 =bi +((ai +Fi(bi,ci,di)+wi+ti)<<<si) di+4=ai+((di+Fi+1(ai,bi,ci)+wi+1+ti+1)<<<si+1) ci+4=di+((ci+Fi+2(di,ai,bi)+wi+2+ti+2)<<<si+2) bi+4=ci+((bi+Fi+3(ci,di,ai)+wi+3+ti+3)<<<si+3) ti and si are predefined step dependant constants
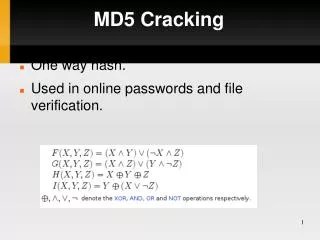
The Non-Linear Functions • Fi changes every 16 steps Fi(X,Y,Z)=(X^Y)ν(~X^Z) 0≤i ≤15 Fi(X,Y,Z)=(X^Z) ν(Y^~Z) 16 ≤i ≤31 Fi(X,Y,Z)=X Y Z 32 ≤i ≤47 Fi(X,Y,Z)=Y (X ν ~Z) 48 ≤i ≤63 This provides non-linearity so you can not extract the message from the hash
Finding Collisions • MD5 has a 128 bit hash so a brute force attack to find a collision requires at most 2128 applications of MD5 and 264 by the birthday paradox • Xiaoyun Wang and Hongbo Yu have an attack that requires 239 operations • This attack takes at most an hour and 5 minutes on a IBM P690 (supercomputer)
Recall: Differential Cryptanalysis • Find a particular ∆M such that a particular ∆H occurs with high probability • In collision case, want ∆H = 0.
Differentials • The attack uses two types of differentials • XOR differential: ΔX=X X’ • Modular differential: ΔX=X-X’ mod 232 • For M=(m0,…,mn-1) and M’=(m’0,…m’n-1) the full hash differential is for a message of length 512n bits ΔH0 -> ΔH1 ->…-> ΔHn= ΔH If M and M’ are a collision pair ΔH=0
Round differentials • ΔHi -> ΔHi+1 can be split into round differentials as well • ΔHiΔR0ΔR1ΔR2ΔR3=ΔHi+1 P3 P0 P1 P2
Probability • Each of these differentials has a probabilistic relationship with the next. • Ideally, we’d like to be able to set up 2 messages where we can guarantee with probability 1 that ΔH=0 • This can be assured by modifying M so the first round differential will be what you want • More modifications will improve the probability for the second, third and fourth round differentials • ΔM0 has been picked to improve this as well
The Attack • Find M=(M0,M1) and M’=(M’0,M’1) • ΔM0=M’0-M0=(0,0,0,0,231,0,0,0,0,0,0,215,0,0,231,0) • ΔM1=M’1-M1=(0,0,0,0,231,0,0,0,0,0,0,-215,0,0,231,0) • ΔH1=(231,231+225,231+225,231+225) • i.e. M0 and messages that does this is not a collision • ΔM0 has been picked to improve the probability that the round differentials will hold • M’0 differ in the 5th, 12th and 15th words only • Same for M1 and M’1. • Every set of messages that does this is not a collision • ΔM0 has been picked to improve this as well
Message Modification • It is easy to modify a message word so that the first non-zero step differential (after the 5th step) is anything you want with probability 1 • Modify multiple words to guarantee the round differentials with high probability • Each modification to make one condition hold may make another not hold
Sufficient Conditions • Δw5 is first non-zero differential • At the 8th step Δw5 has affected a, d and c so (Δc2, Δd2, Δa2, Δb1 )-> Δb2 since Δb1=0 • There are 13 conditions on a2, c2 and d2 that will guarantee Δb2 to be whatever you like with high probability • Each characteristic has between 1 and 28 conditions for 30 characteristics for M0 and 29 characteristics with between 2 and 25 conditions for M1 for well over 200 conditions
Conditions for bi b1,7 = 0 b1,8 = c1,8 b1,9 = c1,9 b1,10 = c1,10 b1,11 = c1,11 b1,12 = 1 b1,13 = c1,13 b1,14 = c1,14 b1,15 = c1,15b1,16 = c1,16 b1,17 = c1,17 b1,18 = c1,18 b1,19 = c1,19 b1,20 = 1 b1,21 = c1,21b1,22 = c1,22 b1,23 = c1,23 b1,24 = 0 b1,32 = 1
Technique for M0 • Select random M0 • Modify M0 so as many of the conditions hold as possible • Create M0’=M0+ ΔM0 • This will result in ΔH1 with probability 2-37 • Test this works • This doesn’t require more then 239 MD5 operations
Technique for M1 • Select a random message M1 • Modify M1 so it meets the conditions • M1’ =M1+ ΔM0 • Starting with ΔH1 as IV the probability that H(M1)=H(M1’) is 2-30 • Test the pair of messages for collisions
Creating More Collisions • There are many M1s that will collide with any properly crafted M0 • You can also change the last two words of M0 and maintain the conditions • This reduces the amount of work needed
Actual Collisions M0 = 2dd31d1 c4eee6c5 69a3d69 5cf9af98 87b5ca2f ab7e4612 3e580440 897ffbb8 634ad55 2b3f409 8388e483 5a417125 e8255108 9fc9cdf7 f2bd1dd9 5b3c3780 M1=d11d0b96 9c7b41dc f497d8e4 d555655a c79a7335 cfdebf0 66f12930 8fb109d1 797f2775 eb5cd530 baade822 5c15cc79 ddcb74ed 6dd3c55f d80a9bb1 e3a7cc35 M0’=2dd31d1 c4eee6c5 69a3d69 5cf9af98 7b5ca2f ab7e4612 3e580440 897ffbb8 634ad55 2b3f409 8388e483 5a41f125 e8255108 9fc9cdf7 72bd1dd9 5b3c3780 M1’=d11d0b96 9c7b41dc f497d8e4 d555655a 479a7335 cfdebf0 66f12930 8fb109d1 797f2775 eb5cd530 baade822 5c154c79 ddcb74ed 6dd3c55f 580a9bb1 e3a7cc35 Hash: 9603161f a30f9dbf 9f65ffbc f41fc7ef
References • How To Break MD5 and Other Hash Functions – Xiaoyun Wang and Hongbo Yu (they did the SHA-1 break as well) • Guide to Hash Functions http://unixwiz.net/techtips/iguide-crypto-hashes.html • Cryptographic Hash Lounge (lists what functions have been broken and links to how) http://planeta.terra.com.br/informatica/paulobarreto/hflounge.html • Questions?