1 / 96

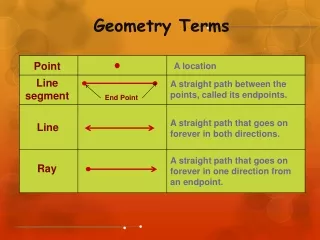
Point

A point is an object with no dimension It is an exact location. A point is named by a capital letter. Point. A. Point A. A line is a straight path that extends without end in one dimension or two opposite directions. Line. l. A. B. Line l or AB.

prema
Télécharger la présentation

Point

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. A point is an object with no dimension It is an exact location. A point is named by a capital letter. Point A Point A

  2. A line is a straight path that extends without end in one dimension or two opposite directions Line l A B Line l or AB

  3. Points are said to be collinear points if they are on the same line Collinear l A B Line l or AB

  4. A plane is a flat surface that extends without end in two dimensions A M C B Plane Plane M or plane ABC

  5. Points are said to be coplanar if they are on the same plane A M C B Coplanar Plane M or plane ABC

  6. The line segment is made up of two endpoints and all the points between the endpoints. Line segment A B Segment AB l B A Line l or AB

  7. A ray has one initial point. From that point, the ray extends without end in one direction only. Ray A B Ray AB l B A Line l or AB

  8. Two rays are opposite rays if they go in exactly opposite directions, forming a line Opposite Rays l B C A Line l or AB

  9. Warm-Up • Name all line segments and rays. A F Z K B

  10. Intersection • Geometric figures intersect if they have one or more points in common Line l Line k F E A D B C

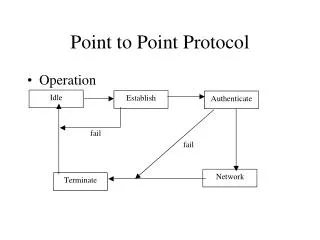
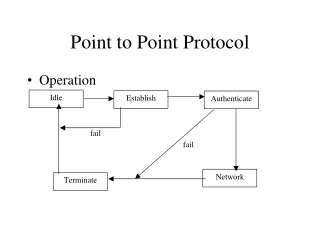
  11. Rules of Intersection • The intersection of two lines is a point • The intersection of two planes is a line

  12. Postulates, Axioms, and Theorems • Postulate or axiom—a rule accepted without proof • Theorem—a statement that can be proven using other rules • Example: Axiom—Two points determine a line

  13. Practice

  14. Ruler Postulate • Coordinate—a real number value assigned to a point • The distance between A and B is AB = | x2 – x1 | A B x1 x2

  15. Segment Addition Postulate • If C is a point between A and B, then AB + BC = AC • If AB + BC = AC, then C is a point between A and B

  16. Practice • P. 14 #48-51 • P. 15 #62-67 • P. 21 #23-33

  17. Warm-Up Sketch the figure. • 1) A line and a plane that do not intersect. • 2) Two planes that do not intersect and a line that intersects each plane in one point. Simplify. • 3) |4-7| 4) √(4+32)

  18. ?s

  19. The Coordinate Plane • Recall the definition of coordinate. • The coordinate plane is a grid wherein points are assigned two values

  20. Plotting Points • Plot the points • A(3,-5) • B(1,-2) • C(3,0) • D(-4,0)

  21. The Distance Formula • If A(x1 , y1) and B (x2 , y2) are points in a coordinate plane, then the distance between them is defined as:

  22. Example • You are given points A(-1,1), B(-4,3), and C(3,2). Find the distance between each pair of points.

  23. Additional Example

  24. Practice • P. 22 #34-42 even

  25. Midpoint And Bisectors • Bisect—To divide an object into two equal parts • A bisector is segment, ray, line, or plane the bisects and object • Midpoint—a point on a line segment that bisects the segment

  26. Midpoint And Coordinates • When provided with points on a coordinate plane, we can find the midpoint between them. • Midpoint Formula: • If A(x1 , y1) and B (x2 , y2) are points in a coordinate plane, then the midpoint between them is defined as:

  27. Example • Given points A(-2,3) and B(5,-2), find the midpoint of segment AB.

  28. Example • The midpoint of segment XY is M(3,-4). One endpoint of the segment is Y(-3,-1). Find the coordinate of X.

  29. Additional Example

  30. Practice • P. 38 #18-30 even

  31. Homework

  32. Warm-Up 1) Find the value of x.--> 2) Find the distance between points (3,1) and (3,-5). 3) Points A, D, F, and X are on a segment in order. AD = 15, AF =22, and AX = 30. a) DF = b) FX =

  33. ?s

  34. Study for Quiz • Take 3 minutes and study for the vocab quiz.

  35. Perimeter, Circumference, Area

  36. Rectangles

  37. Example • Find the perimeter and area of a rectangle that is 12 inches long and 5 inches wide.

  38. Practice Problem • Find the perimeter and area of a rectangle of length 4.5 m and width 0.5 m.

  39. Example—Word Problem • You are planning to build a deck along two sides of a pool. The pool measures 18 ft by 12 ft. The deck will be 8 ft wide. What is the area of the deck?

  40. Challenging Practice • You are designing a mat for a picture. The picture is 8 inches wide and 10 inches tall. The mat is to be 2 inches wide. What is the area of the mat?

  41. Additional Example

  42. Triangles

  43. Example • Find the area of the triangle. 8 9

  44. Example—Graphing • Find the area and perimeter of the triangle defined by points D(1,3), E(8,3), and F(4,7)

  45. Practice • Find the area and perimeter of the triangle defined by points H(-2,2), J(3,-1), and K(-2,-4).

  46. Circles

  47. Example • Find the area and circumference of a circle with a radius of 5 in. • Find the radius of a circle if the circumference is approx. 56.5 cm.

  48. Example • A circle has a diameter of 8 cm. Find the radius, circumference, and area.

More Related