1 / 5

Measuring Angles

This text explores the fundamentals of measuring angles in geometry. It defines angles as formed by two rays sharing a common endpoint, known as the vertex. Key types of angles include acute, right, obtuse, and straight angles. The text also covers congruent, vertical, adjacent, complementary, and supplementary angles. Furthermore, it introduces the Protractor Postulate and Angle Addition Postulate, which help in determining angle measurements and relationships between angles. Understanding these concepts is essential for mastering angle properties in geometry.

rene
Télécharger la présentation

Measuring Angles

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

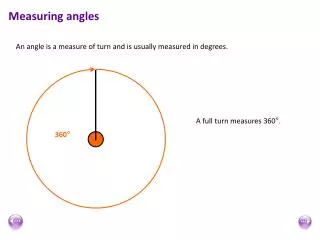
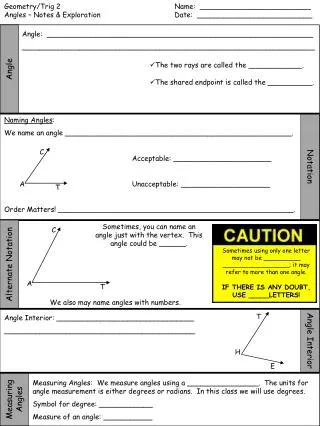
  1. Measuring Angles Angle – formed by two rays with the same endpoint. The rays are the sidesof the angle. The endpoint is the vertexof the angle.

  2. Vocabulary • Acute angle – 0 <x < 90 • Right angle – x = 90 • Obtuse angle– 90 < x < 180 • Straight angle – x = 180 • Congruent angles– angles with the same measure

  3. Vocabulary Continued … • Vertical angles – two angles whose sides are opposite rays. • Adjacent angles – two coplanar angles with a common side, a common vertex, and no common interior points. • Complementary angles – two angles whose measures have a sum of 90. • Supplementary angles – two angles whose measures have a sum of 180.

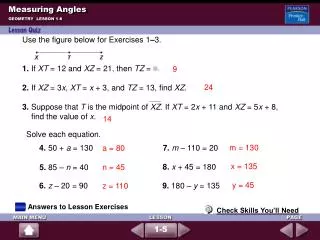
  4. Postulate 1 – 7 Protractor Postulate • Let ray OA and ray OB be opposite rays in a plane. Ray OA, ray OB and all the rays with endpoint O that can be drawn on one side of line AB can be paired with the real numbers from 0 to 180 so that • a. Ray OA is paired with 0 and ray OB is paired with 180. • b. If ray OC is paired with x and ray OD is paired with y, then m < COD = lx – yl.

  5. Postulate 1-8Angle Addition Postulate • If point B is in the interior of < AOC, then the m <AOB + m < BOC = m < AOC • If < AOC is a straight angle, then the m < AOB + m < BOC = 180.

More Related