1 / 22

AVL Tree

AVL Tree. 2. 1. 3. 2. 1. 6. 2. 5. 6. 4. 1. 4. 6. 5. 3. 5. 4. 3. Ordinary Binary Search Tree. Searching time is O( height )  log 2 n   height  n – 1 Speed of search depends on luck. . Best time. Better time. Like a Linked List. e. h L. h R. AVL Tree.

reuel
Télécharger la présentation

AVL Tree

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. AVL Tree

  2. 2 1 3 2 1 6 2 5 6 4 1 4 6 5 3 5 4 3 Ordinary Binary Search Tree • Searching time is O(height) • log2n  height n – 1 Speed of search depends on luck. Best time Better time Like a Linked List

  3. e hL hR AVL Tree AVL : Adelson-Velskii and Landis • AVL = Binary Search Tress + Rule on height For each and every node, e

  4. 1 -1 1 -1 2 0 0 -1 -1 -1 -1 -1 0 1 1 -1 0 -1 -1 -1 -1 -1 -1 1 2 -1 2 1 -1 -1 1 2 AVL Tree examples Null tree has height = -1

  5. Are these AVL?????? AVL Non-AVL

  6. BST from 1000 random data BST and AVL comparison AVL from 1000 random data

  7. Fh Fh – 2 Fh – 1 Finding the height of AVL tree • LetFh be an AVL Tree of height h that has the lowest possible number of nodes. F0 F1 F2 F3 F4 |Fh| = 1 + |Fh–1| + |Fh–2| Fibonacci Tree

  8. Height of Fibonacci Tree AVL tree that has nnodes will have its height <= 1.44 log2n log2n  hAVL 1.44 log2n

  9. 2 2 5 1 5 1 5 2 0 6 6 6 3 0 3 1 3 8 8 8 8 Maintaining the property of AVL 6 9 • Add and remove just like BST. • But adding or removing can cause the tree to lose its AVL property. • We need to rearrange the tree then. 9

  10. AVL Node class AVLNode{ Comparable data; int height; AVLNode left; AVLNode right; AVLNodeAVLNode(Comparable d, AVLNode left, AVLNode right) { data = d; this.left= left; this.right= right; height = 0; } public static intgetHeightAVLNode(AVLNode n) { // the height of null is -1 return (n == null ? -1 : n.height); } Each node has its height information

  11. AVL Node (cont.) -1 +1 0 +2 -2 public static void updateHeightAVLNode(AVLNoden) { if (n==null){return;} //do nothing inthL = getHeightAVLNode(n.left); inthR = getHeightAVLNOde(n.right); n.height= 1 + (hL > hR ? hL : hR); } public static intbalanceValue(AVLNode n) { if (n==null){return 0;} return getHeightAVLNode(n.right) – getHeightAVLNode(n.left); }

  12. 20 10 10 20 99 5 5 99 Rotation • Rotation preserves all properties of BST. r r 15 15 rotateLeftChild(r) rotateRightChild(r)

  13. newRoot 20 10 20 10 5 99 rotateLeftChild( r ) 15 99 5 15 public static AVLNoderotateLeftChild(AVLNode r) { AVLNodenewRoot = r.left; r.left= newRoot.right; newRoot.right= r; updateHeightAVLNode(newRoot.right); updateHeightAVLNode(newRoot); return newRoot; } (1) r newRoot

  14. newRoot 10 20 10 20 99 5 rotateRightChild( r ) 15 5 99 15 public static AVLNoderotateRightChild(AVLNode r) { AVLNodenewRoot = r.right; r.right= newRoot.left; newRoot.left= r; updateHeightAVLNode(newRoot.left); updateHeightAVLNode(newRoot); return newRoot; } (1) r newRoot

  15. Add and remove use rebalance class AVLTree{ AVLNode n; public AVLTree(){ n = null; } AVLNodeinsertAVL(AVLNoder, DType x) { … //same as insert in BST r = rebalance(r); return r; } AVLNoderemoveAVL(AVLNoder, DType x) { ... // same as remove in BST r = rebalance(r); return r; }

  16. 5 5 r 2 x 2 2 6 6 1 5 C 1 1 B 3 3 A 0 3 6 0 x r rebalance : 1st case A C B rotateLeftChild(r)

  17. 3 3 r 5 x 5 5 2 2 6 3 C 6 6 B 4 4 A 9 4 2 9 x r A rebalance : 2nd case C B rotateRightChild(r)

  18. 5 5 5 2 6 3 6 2 6 3 1 3 2 4 1 3 2 5 1 4 4 6 1 r r y y x r x D D y x C A A D B rebalance : 3rd case C A B C B rotateRightChild(r.left) rotateLeftChild(r)

  19. 2 2 2 5 1 4 1 5 1 4 6 4 5 3 6 4 5 2 6 3 3 1 6 r r y y x r x A A y x B D D A C rebalance : 4th case B D C B C rotateLeftChild(r.right) rotateRightChild(r)

  20. r r x x C C B B rotateLeftChild(r.right) rotateRightChild(r) A A rotateRightChild(r) r r x x D A y y D A rebalance C B B C rotateLeftChild(r) AVLNode rebalance(AVLNoder) { if (r == NULL) return r; int balance = balanceValue(r); if (balance == -2) { if (balanceValue(r.left) == 1) r.left= rotateRightChild(r.left); r = rotateLeftChild(r); } else if (balance == 2) { if (balanceValue(r.right) == -1) r.right= rotateLeftChild(r.right); r = rotateRightChild(r); } setHeightAVLNode(r); return r; } (1) rotateRightChild(r.left) rotateLeftChild(r)

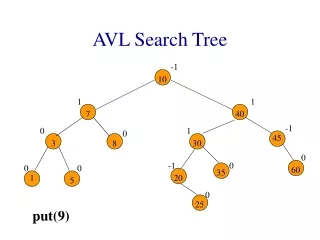
  21. 2 2 2 1 2 1 1 3 1 3 1 3 2 1 6 2 6 6 3 8 3 8 2 3 3 2 1 3 2 6 2 6 1 6 6 1 1 8 4 8 8 4 3 8 4 15 4 3 3 3 EXAMPLE 2 6 2 6 2 6 1 8 4 1 4 14 1 8 4 14 8 15 15 15 14 1, 2, 3, 6, 8, 4, 15, 14 1

  22. Conclusion • AVL tree is a Binary Search Tree with height constraint. • It is proven thatlog2n  h <1.44 log2n • Each node stores its height. • Insert/remove,then rebalance • Rebalance = rotation • Add, remove, search takeO(log n)

More Related