1 / 14

Understanding Triangle Angle Measures and Theorems: A Guide for Students

This resource explores key concepts in triangle geometry, including the Triangle Angle-Sum Theorem, Vertical Angles Theorem, and the Exterior Angle Theorem. It provides examples of how to apply these theorems to find measures of unknown angles in various triangle configurations, using both direct computation and logical reasoning. Students will learn how to validate their answers by checking that the angles of a triangle sum to 180 degrees. This guide is designed to help improve understanding of geometric principles and enhance problem-solving skills in triangle-related contexts.

sakura
Télécharger la présentation

Understanding Triangle Angle Measures and Theorems: A Guide for Students

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

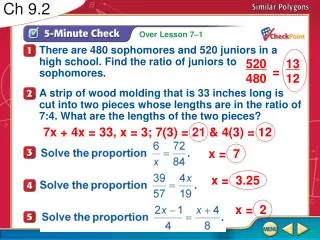
  1. BELLRINGER:1) Classify ΔRST .2) Find y if ΔRST is an isosceles triangle withRS  RT. 5-Minute Check 1

  2. Concept 1

  3. Use the Triangle Angle-Sum Theorem SOFTBALL The diagram shows the path of the softball in a drill developed by four players. Find the measure of each numbered angle. Understand Examine the information in the diagram. You know the measures of two angles of one triangle and only one measure of another. You also know that 1 and 2 are vertical angles. Example 1

  4. Use the Triangle Angle-Sum Theorem Plan Find m1 first because the measure of two angles of the triangle are known. Use the Vertical Angles Theorem to find m2. Then you will have enough information to find the measure of 3. Solve Triangle Angle-Sum Theorem Simplify. Subtract 117 from each side. Example 1

  5. Use the Triangle Angle-Sum Theorem 1 and 2 are congruent vertical angles. So, m2 = 63. Triangle Angle-Sum Theorem Simplify. Subtract 142 from each side. Answer: Therefore, m1 = 63, m2 = 63, and m3 = 38. CheckThe sums of the measures of the angles in each triangle should be 180.m1 + 43 + 74 = 63 + 43 + 74 or 180m2 + m3 + 79 = 63 + 38 + 79 or 180 Example 1

  6. Find the measure of 3. A. 95 B. 75 C. 57 D. 85 Example 1

  7. Concept 3

  8. Use the Exterior Angle Theorem GARDENING Find the measure of FLW in the fenced flower garden shown. mLOW + mOWL = mFLW Exterior Angle Theorem x + 32 = 2x – 48 Substitution 32 = x – 48 Subtract x from each side. 80 = x Add 48 to each side. Answer: So, mFLW = 2(80) – 48 or 112. Example 2

  9. The piece of quilt fabric is in the shape of a right triangle. Find the measure of ACD. A. 30 B. 40 C. 50 D. 130 Example 2

  10. Concept 5

  11. m1 = 48 + 56 Exterior Angle Theorem = 104 Simplify. If 2 s form a linear pair, they are supplementary. 104 + m2 = 180 Substitution 76 Subtract 104 from each side. Find Angle Measures in Right Triangles Find the measure of each numbered angle. Example 3

  12. m 3 = 90 – 48 If 2 s form a right angle, they are complementary. = 42 Simplify. Triangle Angle-Sum Theorem (90 – 34) + m2+ m 4 = 180 56 + 76 + m 4 = 180 Substitution Simplify. 132 + m4 = 180 48 Subtract 132 from each side. Find Angle Measures in Right Triangles Example 3

  13. m5 + 41 + 90 = 180 Triangle Angle-Sum Theorem m5 + 143 = 180 Simplify. 49 Subtract 131 from each side. m1 = 104,m2 = 76, m3 = 42,m4 = 48, m5 = 49 Find Angle Measures in Right Triangles Example 3

  14. Find m3. A. 50 B. 45 C. 85 D. 130 Example 3

More Related