Tutorial 00 Analysis with HEP Objects
130 likes | 152 Vues
Learn about the different types of objects in CLHEP, such as 3 and 4 vectors, displacement vectors, Lorentz boosts and rotations, and 3D transformations. Use these objects to perform physics calculations like invariant mass and impact parameter.

Tutorial 00 Analysis with HEP Objects
E N D
Presentation Transcript
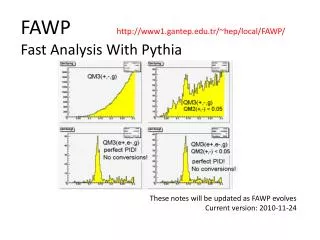
Tutorial 00Analysis with HEP Objects • URL with complete information: • http://cdfpca.fnal.gov/CdfCode/source/CLHEP/doc/html/0CLHEP.html • Small overview of what types of Objects exist • 3 and 4 vectors, displacement vectors • Lorentz boosts and rotations • 3D transformations. • Using these objects to do some typical physics calculations • Invariant mass • Impact parameter between a vector and a point in space. • Helicity angle in Dsfp • Transversity angle in B J/yf • “addpkg Examples” and look in TUTORIAL00/
Types of Objects in CLHEP • Hep3Vector A(ax, ay, az), B(bx, by, bz); • The vector A can be initialized with double’s. • Add and subtract these vectors, scalar multiplication • Double d; • Hep3Vector C = d*A + B/d; • Take the dot product: • Double ABcostheta = A.dot(B); • Take the cross product: • Hep3Vector AcrossB = A.cross(B); • Find the Unit vector in the same direction as vector A. • Hep3Vector UnitA = A.unit(); • Find Magnitude of the Vector A: • HepDouble MagA = A.mag();
Types of Objects in CLHEP • LorentzVector A(px, py, pz, Ea), B(px, py, pz, Eb); • The Lorentz vector A can be initialized with double’s. • Add and subtract these vectors, scalar multiplication • Double d; • LorentzVector C = d*A + B/d; • Find the Mass of A or of the combination • HepDouble mass = A.m(); • HepDouble invmass = (A+B).m(); • Get 3-vector direction of the Lorentz vector • Hep3Vector Adir = A.vect(); • Four Vector dot product • HepDouble invariantC = A.dot(B); • Find Boost vector in for this object • Hep3Vector velocityA = A.boostVector();
? Impact parameter: vector to a point. Given a position and direction of particle, what is the Impact Paramter?
? Impact parameter: vector to a point. #include "CLHEP/Geometry/Point3D.h" #include "CLHEP/Geometry/Vector3D.h" int main(int, char **) { HepPoint3D pointOnTrack; HepPoint3D pointInSpace; HepVector3D directionOfTrack; // Impact parameter in three D: HepVector3D impactVect = (pointOnTrack - pointInSpace).cross(directionOfTrack); double i2d = impactVect.z(); double i3d = impactVect.mag(); }
Transformations: Different kinds of Transformations: HepTransform3D, HepTranslate3D, HepRotateX3D, HepRotateY3D, HepReflectX3D, HepScale3D… Can compose, e.g: HepTransform3D xform= HepTranslate3X3(5.0)*HepRotateY3D(M_PI)*HepRotateZ3D(M_PI/2); Can invert: HepTransform xformInverse = xform.inverse();
Hep3Vector Three kinds of vectors: Point (affected by translation, rotations, reflections) Vector(affected by rotations and reflections) Normal(affected by rotations) All of these have exactly the same functions as Hep3Vector Each give a different result when transformed E.G Move the origin of coordinates by 1 mm, due to a beam spot shift: HepPoint3D pointOnTrack; HepPoint3D pointInSpace; HepVector3D directionOfTrack; HepTranslate3D shift(0.1); HepPoint3D pOTPrime = shift*pointOnTrack; // moves! HepPoint3D pISPrime = shift *pointInSpace; // moves! HepVector3D doTPrime = shift *directionOfTrack; // does not move! HepNormal3D HepPoint3D HepVector3D
Lorentz transformations: * Act on Lorentz transfomations, Lorentz vectors * Many ways to construct: Most useful: from a vector that gives (bx, by, bz) Can get this from a fourVector: // Get the 3-velocity of phi in the lab frame: Hep3Vector phiVelocity = Phi.boostVector(); // Create a boost from the Phi Rest Frame to the Lab: HepLorentzRotation phiBoost(phiVelocity); * Can invert: // Create a boost from the Lab to the Phi Rest Frame; HepLorentzRotation toPhiRest = phiBoost.inverse(); * More specialized: // Create a boost from B Rest Frame to D Rest Frame; HepLorentzRotation BToD = boostToD*boostToB.inverse();
K+K- K- p- K+ Helicity Angle: Dsfp Angle of p- wrt the K- in the f rest frame
K- Ds- K+ Helicity Angle: Dsfp // Get these vectors from the tracks, in the lab frame: HepLorentzVector KPlus; HepLorentzVector KMinus; HepLorentzVector PiMinus; // Compute the Phi Four Momentum: HepLorentzVector Phi = KPlus + KMinus; // Get the D Four vector: HepLorentzVector Ds = Phi+PiMinus; // Get the 3-velocity of phi in the lab frame: Hep3Vector phiVelocity = Phi.boostVector(); // Create a boost to the rest frame of the phi: HepLorentzRotation phiBoost(phiVelocity); HepLorentzRotation toPhiRest = phiBoost.inverse(); // Get the direction of the KMinus and the pion in the phi rest frame: Hep3Vector KMPrimeDir = (toPhiRest*KMinus).vect().unit(); Hep3Vector DsPrimeDir = (toPhiRest*Ds).vect().unit(); double cosHelicity = KMPrimeDir.dot(DsPrimeDir);
K+K- Bs J/f K+ m+ m- x f z K- 1- Transversity Angle Angle between m+ and the normal to the K+K- plane in the J/rest frame
Transversity Angle // Get these vectors from the tracks, in the lab frame: HepLorentzVector KPlus; HepLorentzVector KMinus; HepLorentzVector MuPlus; HepLorentzVector MuMinus; // Compute the JPsi Four Momentum: HepLorentzVector JPsi = MuPlus + MuMinus; // Get the 3-velocity of J/psi in the lab frame: Hep3Vector JPsiVelocity = JPsi.boostVector(); // Create a boost to the rest frame of the J/psi: HepLorentzRotation JPsiBoost(JPsiVelocity); HepLorentzRotation toJPsiRest = JPsiBoost.inverse(); // Find the Kaon and Muon direction vectors in the J/psi rest frame Hep3Vector KPlusPrime = (toJPsiRest*KPlus).vect(); Hep3Vector KMinusPrime = (toJPsiRest*KMinus).vect(); Hep3Vector MuPlusPrime = (toJPsiRest*MuPlus).vect(); // Compute the transversity angle: double cosTransversity = KMinusPrime.cross(KPlusPrime).unit().dot(MuPlusPrime.unit()); Angle between m+ and the normal to the K+K- plane in the J/rest frame
To be continued: class CdfTrack { Hep3Vector getMomentum() const; HepLorentzVector getFourMomentum() const; + more! };