1 / 20

Estimating and Testing  2

Estimating and Testing  2. (n-1)s 2 / 2 has a  2 distribution with n-1 degrees of freedom. Like other parameters, can create CIs and hypothesis tests since we know the distribution. 0. Estimating and Testing  1 2 /  2 2.

seda
Télécharger la présentation

Estimating and Testing  2

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

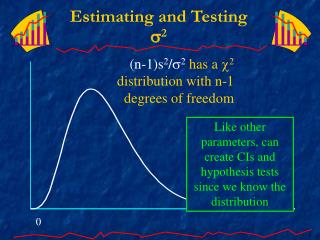
  1. Estimating and Testing 2 (n-1)s2/2 has a 2 distribution with n-1 degrees of freedom Like other parameters, can create CIs and hypothesis tests since we know the distribution 0

  2. Estimating and Testing 12 /22 12/22has an F distribution with n1-1 and n2-1 d.f. Like other parameters, can create CIs and hypothesis tests since we know the distribution 0

  3. One-Way ANOVA • Example • As a training specialist, you want to determine whether three different training methods are equally effective so you want to compare the mean time to complete a task after individuals are trained with the three different methods. (Random variable: completion time) • One-Way ANOVA hypothesis test • H0: 1 = 2 = 3 = . . . = k • HA: The means are not all equal (at least one pair differs from each other) • Three Requirements • k independent random samples • Random variables are normally distributed • Equal population variances for the random variables

  4. One-Way ANOVA Data Set x1,1 x1,2 x1,3 … x2,1 x2,2 x2,3 … xk,1 xk,2 xk,3 … _ _ _

  5. One-Way ANOVA • One-Way ANOVA hypothesis test • H0: 1 = 2 = 3 = . . . = k • HA: The means are not all equal (at least one pair differs from each other) • Test Statistic • F = BSV / WSV with k-1, nT-k d.f. • Decision Rule • Reject H0 if F > F • Intuition • If BSV is “large” then H0 is unlikely to be true Note: Always one-tailed and >

  6. F Distribution P(F < ) = 0.95 9 and 10 d.f P(F > ) = 0.05 0 ?

  7. Select F Distribution 5% Critical Values Denominator Degrees of Freedom

  8. One-Way ANOVA: Example • H0: 1 = 2 = 3 • HA: The means are not all equal • Test Statistic • F = BSV / WSV with k-1,nT-k d.f. • Decision Rule • Reject H0 if F > F • Intuition • If BSV is “large” then H0 is unlikely to be true _ =

  9. One-Way ANOVA: Another Example • H0: 1 = 2 = 3 • HA: The means are not all equal • Test Statistic • F = BSV / WSV with k-1,nT-k d.f. • Decision Rule • Reject H0 if F > F • Intuition • If BSV is “large” then H0 is unlikely to be true _ =

  10. Data Analysis: ANOVA-Single Factor

  11. Two-Way ANOVA • Example • Suppose 10 individuals are asked to judge the taste quality of three beers: Budweiser, Bass Ale, and London Pride. Based on some complicated rating system, each individual assigns a numerical score to each beer (all 10 individuals taste each of the three beers). • Note that we now have two factors: raters and beers • Questions • Is the average taste rating equal for each beer? • Is the average taste rating equal for each rater? • Can do an ANOVA hypothesis test for each question: • H0: 1 = 2 = 3 = . . . = k • HA: The means are not all equal (at least one pair differs from each other)

  12. Two-Way ANOVA: Example • Suppose 10 individuals are asked to judge the taste quality of three beers: Budweiser, Bass Ale, and London Pride. Based on some complicated rating system, each individual assigns a numerical score to each beer (all 10 individuals taste each of the three beers). Once the data are collected, you estimate the following ANOVA table:

  13. Another Example • These data values were obtained from a randomized block design experiment. • First, Pretend that these data were collected using a completely randomized design. Can we conclude at the 5% significance level that there are differences in the treatment means? • How does your answer change if you account for the randomized block design?

  14. Pretend One-Way

  15. But is Actually Two-Way

  16. One-Way ANOVA via Regression “Stack” data using dummy variables

  17. One-Way ANOVA via Regression

  18. The RegressionANOVA Table F test for: Ho: 1= 2 = … = k = 0 (excluding the intercept) HA: at least one i0

  19. Regression and Two-Way ANOVA Blocks “Stack” data using dummy variables

  20. Regression and Two-Way ANOVA Source | SS df MS Number of obs = 15 ----------+---------------------- F( 6, 8) = 28.00 Model | 338.800 6 56.467 Prob > F = 0.0001 Residual | 16.133 8 2.017 R-squared = 0.9545 -------------+------------------- Adj R-squared = 0.9205 Total | 354.933 14 25.352 Root MSE = 1.4201 ------------------------------------------------------------- treatment | Coef. Std. Err. t P>|t| [95% Conf. Int] ----------+-------------------------------------------------- b | -2.600 .898 -2.89 0.020 -4.671 -.529 c | -3.000 .898 -3.34 0.010 -5.071 -.929 b2 | -1.333 1.160 -1.15 0.283 -4.007 1.340 b3 | 6.667 1.160 5.75 0.000 3.993 9.340 b4 | 9.667 1.160 8.34 0.000 6.993 12.340 b5 | -1.333 1.160 -1.15 0.283 -4.007 1.340 _cons | 10.867 .970 11.20 0.000 8.630 13.104 ------------------------------------------------------------- Need Partial F test (later in course)

More Related